ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Question équilatérale...      niveau 5è

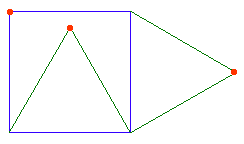
Cette figure géométrique présente un carré et deux triangles équilatéraux, l'un dans le carré, l'autre à l'extérieur. Chacun d'eux emprunte un côté du carré.

Si cela vous parait bien clair, il est temps de passer à la question. Mais au fait :

Quelle est la question ?...
 

 Si tu sèches après avoir bien cherché :  ››››

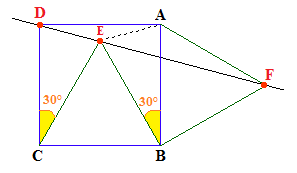
 ➔   La question était, et vous l'aviez surement trouvée :

Montrer que les points rouges sont alignés

C'est à dire ici que D, E et F sont situés sur une même droite.

Pour prouver cela, il suffit d'établir que :

• Notons tout d'abord que CD = CE = BE = BA = BF : mesure des côtés des triangles équilatéraux construits à partir du carré.
   
• Le triangle DCE est isocèle, donc, dans ce triangle, ^D = ^E et comme ^ECD = 90° - 60° = 30°, on a :
• ^DEC = ^EDC = 150°/2 = 75°.
   
• ^CEB = 60° puisque le triangle CEB est équilatéral.
   
• Enfin, EBF est un triangle rectangle isocèle car d'une part BE = BF et, d'autre part : ^EBF =  ^EBA + ABF = (90°- 60°) + 60° = 90°
  Par suite, ^FEB = 45°.

Conclusion :   

^DEC + ^CEB + ^BEF = 75 ° + 60° + 45° = 180°.

Ce qu'il fallait démontrer : les points D, E et F sont alignés.