Le puits et la maison

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Le puits & la maison Outils : Dérivation - Fonction irrationnelle à minimiser TD 1èreS/TerS

➔ Ce problème est une variante du problème La Jeep et le lac où une solution trigonométrique est proposée.
Une étude analytique est ici suggérée.

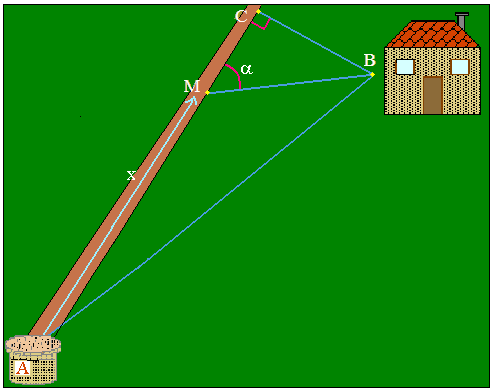
Vous possédez une maison en rase campagne assez éloignée d'un puits et désirez réaliser une adduction d'eau au moyen d'une pompe électrique.

Vous pouvez suivre le chemin ou passer directement à travers champ. Mais le champ étant cultivé, il faudra enterrer les tuyaux plus profondément qu'en longeant le chemin :

• 100 m de canalisation vous coûteront 500 € à travers champ
et 400 € en suivant le chemin.

• On donne : AC = 1000 m; BC = 200 m, ^ACB = 90°.

Sur quelle distance a-t-on intérêt à suivre la route ?

! On a tendance à répondre : "il faut longer la route le plus possible"... Faux !

Indications : on note M le point où l'on quitte la route. Si l'on doit suivre la route le plus possible, la solution serait en C. Montrons qu'il n'en est rien :

1°/ Utiliser l'hectomètre comme unité de distance et 100 € comme unité de coût et montrer que le coût s'exprime par :

2°/ Montrer que f'(x) est du signe de :

et, en remarquant que x - 10 est négatif, justifier que g(x) est du signe de :

-9x²+ 180x - 836

3°/ Établir le tableau de variation de f. En déduire le point M optimal.

Si vous séchez après avoir bien cherché : ››››

Éléments de réponse :

1°/ Avec les unités choisies, on a BC = 2 et, puisque AM = x, CM = 10 - x. L'usage du théorème de Pythagore dans le triangle rectangle MCB fournit facilement BC sous la forme d'un radical.

Le coût s'obtient en centaines d'euros, par f(x) = 4AM + 5MB, soit :

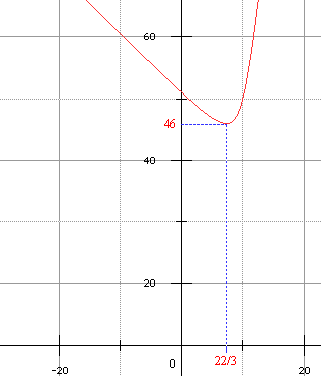
2°/ & 3°/ Le discriminant de g(x) est un carré parfait 24² = 576; en appliquant le signe du trinôme sur l'intervalle [0,10], on trouve aisément que f passe par un minimum absolu sur cet intervalle lorsque x = 10 - 8/3 = 22/3, soit lorsque AM ≅ 773 m.

   ♦ Coût (exact) optimal AM + MB : 4600 €.
   ♦ Coût AB à travers le champ : ≅ 5099 €.
   ♦ Coût AC + CB : 5000 €.

Comme quoi le chemin le plus court n'est pas toujours le moins cher !

On pourra reprendre l'exercice par une méthode trigonométrique cherchant à évaluer l'angle α optimal. Cet angle vérifie cos α = 4/5, ce qui fournit α ≅ 116°.