ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Pythagore + Thalès = M     un problème de construction      niveau 2nde

On donne un cercle de centre O, de rayon r et un point A du cercle. On trace la tangente (t) au point A.

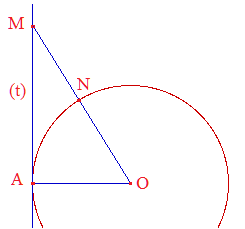
Construire sur (t) le point M distinct de A, de sorte que si on trace [OM] coupant le cercle en N, on obtienne AM = 2MN.

∗∗∗  Coup de pouce :      

Montrer d'abord que si la condition AM = 2MN est réalisée, on doit avoir MN = 2r/3. Construire M reviendra alors à savoir construire le tiers du diamètre du cercle...

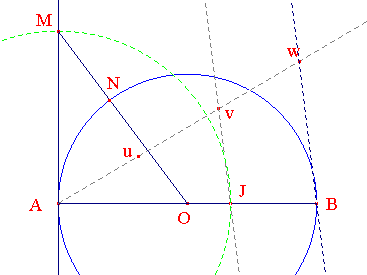
Posons x = MN. Vu que (t) est la tangente en A au cercle, le triangle OAM est rectangle en A.

On a OA = r, OM = r + MN = r + x. Si AM = 2MN = 2x, on peut écrire, par usage du théorème de Pythagore dans le triangle rectangle AOM :

OM² = OA² + AM²

D'où (r + x)² = r² + (2x)², c'est à dire après développement et simplification : 2rx = 3x².

 ➔   x n'est pas nul car sinon M serait sur le cercle confondu avec N, et étant aussi sur (t), il serait en A. On aurait A = M = N et l'énoncé précise A distinct de M.

On peut donc simplifier par x :

x = 2r/3

Soit B le point diamétralement opposé à A. On a  AB = 2r et il nous faut construire M tel que :

AM = 2MN = 4r/3 = 2AB/3

L'usage de la propriété de Thalès permet de construire le point J de [AB] tel que : AJ = 2AB/3 revenant à AJ/AB = 2/3 :

Sur une demi-droite quelconque d'origine A ne passant pas par B, on reporte 3 mesures arbitraires (voir figure). On trace (wB) puis la parallèle à (wB) passant par v coupant [AB] en J.

On a Au/Aw = 2/3 et par conséquent, AJ/AB = 2/3.

On construit ensuite M en traçant le cercle de centre A passant par J.

Et on fait la synthèse, preuve du bien fondé de la construction, très simple ici : OM² = (4r/3)² + r2 = 25r²/9. Donc OM = 5r/3, d'où MN = OM - ON = 5r/3 - r = 2r/3.