Étude des fonctions x → 1 + x² - 2x²ln(x) et x → ln(x)/(1 + x²)

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Étude des fonctions x → 1 + x² - 2x²ln(x) et x → ln(x)/(1 + x²)
(Source modifiée : BacS, Nouvelle Calédonie 2010)

Partie 1 : on considère la fonction numérique φ définie pour tout x de ]0, +∞[ par :

φ(x) = 1 + x² - 2x²lnx.

1°/ a) Montrer que la limite de φ(x) lorsque x tend vers 0 par valeurs positives est égale à 1.

b) On prolonge l'ensemble de définition de φ à [0, +∞[ en posant φ(0) = 1. Calculer la limite du quotient :

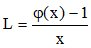
lorsque x tend vers 0 par valeurs supérieures. Quelle est l'interprétation graphique de ce résultat ?

c) Calculer la limite de φ en +∞

2°/ a) On suppose x non nul. Calculer φ'(x). Étudier le sens de variation de φ.

b) Calculer φ(1) et φ(e). Montrer que l'équation φ(x) = 0 admet une unique solution α dans l'intervalle ]1,e[. Déterminer un encadrement de α d'amplitude 0,1 et préciser le signe de φ(x) sur [0, +∞[.

Partie 2 : on considère maintenant la fonction numérique f définie pour tout x de ]0, +∞[ par :

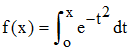
On note f' la fonction dérivée de f.

1°/ Justifier brièvement que f est continue et dérivable sur son ensemble de définition et que sa fonction dérivée f' est du signe de φ.

2°/ a) Déduire des résultats de la partie 1 le sens de variation de f.

b) Calculer les limites de f aux bornes de son ensemble de définition.

3°/ a) à l'aide d'une intégration par parties, calculer l'intégrale :

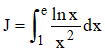
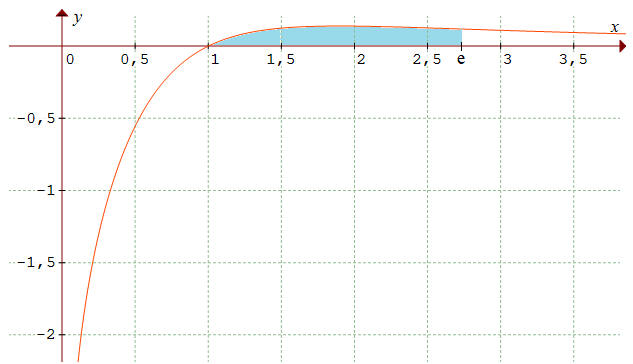
b) La courbe rouge ci-dessous représente les variation de la fonction f sur ]0,+∞[. Donner un encadrement de l'aire colorée en bleu ci-dessous. N.B. e ≃ 2,718 désigne comme à l'accoutumée la base des logarithmes népériens.

➔ La courbe illustrant les variations de f n'est pas exigée. Elle est représentée ci-dessous dans un repère orthonormé d'unité 4 cm :

Si vous séchez après avoir bien cherché : ››››

Solution :

Partie 1 :

1°/ a) φ(x) = 1 + x² - 2x × xlnx. Lorsque x tend vers 0 par valeurs positives, xlnx → 0 (limite de référence).
On en déduit lim_{x→
0}φ(x) = 1.

b) On a L = x - 2xlnx avec xlnx tendant vers 0 par valeurs supérieures. L tend donc vers 0. L peut s'écrire :

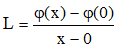
L s'interprète comme la limite du taux d'accroissement de φ au point 0 (x > 0). L est donc le coefficient directeur de la (demi-) tangente en x = 0 à la courbe représentative de φ. Cette limite étant nulle, il s'agit d'une tangente horizontale.

c) On peut écrire φ(x) sous la forme 1 + x² (1 - 2lnx). Lorsque x tend vers +∞, x² et - 2lnx tendent respectivement vers +∞ et -∞. Par conséquent lim_x→ _+∞φ(x) = -∞.

2°/ a) φ est somme et produit de fonctions dérivables sur ]0, +∞[, φ est donc continue et dérivable sur cet intervalle :

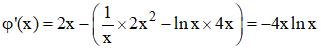
φ'(x) est du signe de - ln x : φ croît sur ]0;1] et décroît sur [1;+∞[.

b) ln 1 = 0, donc φ(1) = 2; ln e = 1, donc φ(e) = 1 - e². Sur l'intervalle [1;e], φ(x) passe continument de φ(1) = 2 > 0 à φ(e) = 1 - e²< 0 en décroissant strictement; par suite, selon le théorème des valeurs intermédiaires, la fonction φ prend une unique fois la valeur 0 en un point α de l'intervalle ]1;e[.

φ(2) = 5 - 8ln2 = - 0,54... < 0 , φ(1,5) = 0,4254... > 0 : α ∈ ]1,5;2]
φ(1,9) = - 0,0242... < 0 , φ(1,8) = 0,4311... > 0 : α est donc compris entre 1,8 et 1,9 :

1,8 < α < 1,9

φ croît de 1 à 2 sur l'intervalle [0,1], décroît de 2 à 0 sur l'intervalle [1,α] et poursuit sa décroissance de 0 à -∞ sur [α,+∞[. Par conséquent, φ est strictement positive sur [0,α[, nulle en α et strictement négative sur ]α,+∞[.

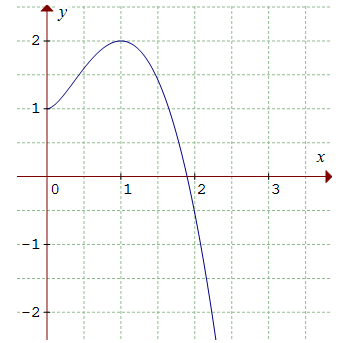
Pour info : représentation des variations de φ

Partie 2 :

1°) Sur ]0,+∞[, f est le quotient de deux fonctions continues et dérivables sur cet intervalle à savoir x → lnx et x → 1 + x². On a alors :

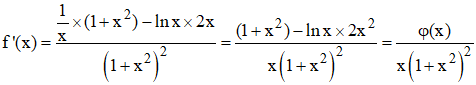
x étant strictement positif, f' est du signe de son numérateur, c'est à dire du signe de φ(x).

2°/ a) Selon la question 2°c) de la partie 1, f croît strictement sur l'intervalle [0,α[, passe par un maximum en α, f(α) ≃ 0,139, puis décroît strictement sur l'intervalle ]α,+∞[.

b) Lorsque x tend vers 0, lnx tend vers -∞ et 1 + x² tend vers 1, donc f a pour limite -∞.
Lorsque x tend vers +∞, on a 0 < f(x) < ln(x)/x² = 1/x × ln(x)/x. Or 1/x et ln(x)/x tendent vers 0 (limites de référence). On en déduit que f a pour limite 0 : l'axe des abscisses est une asymptote horizontale à sa courbe représentative au voisinage de +∞.

3°) On applique la formule d'intégration par parties :

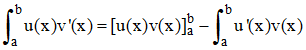
avec u(x) = ln(x), v'(x) = 1/x², u'(x) = 1/x, v'(x) = -1/x. Sur l'intervalle d'intégration ces quatre fonctions sont continues. On peut donc écrire :

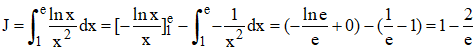
b) Soit (c) la courbe représentative des variations de f. On a vu en 2°b) que l'on a 0 < f(x) < ln(x)/x². Exprimée en unités d'aire (u.a.), l'aire A colorée en bleu est l'aire comprise entre (c) et l'axe des abscisses sur l'intervalle [1,e]. C'est dire que 0 < A < J. Autrement dit :

0 < A < 1 - 2/e

➔ exprimée en cm², 1u.a. = 16 cm², A mesure environ 4,23 cm².