
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
» Source : Bulletin des élèves de mathématiques spéciales - 1er mars 1914
1°/ On demande d'étudier les variations de la fonction y = f(x) définie par :
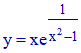
On notera (C) sa courbe représentative dans un repère orthonormé d'unité 2cm. Préciser les limites de f aux bornes de son ensemble de définition (on remarquera que l'on peut restreindre l'étude aux valeurs positives de x).
2°/ Préciser l'allure de (C) au voisinage de 1 et -1.
3°/ Au moyen d'un développement limité, justifier que (C) admet la 1ère bissectrice du repère comme asymptote oblique pour x infini.
➔ On donnera les valeurs calculées arrondies au 1/100è.
Si vous séchez après avoir bien cherché : ››››
| Solution : |
La fonction est définie, continue et
dérivable en tout point de R privé de ± 1. Le changement de x en -x
change y en son opposé.
On se contente donc d'étudier la fonction sur D = R+-
{1} = [0,1[∪]1,+∞[.
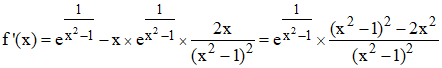
f![]() '(x)
est du signe de (x2 - 1)2 - 2x2 qui se
factorise en (x2 + x√2 - 1)(x2 - x√2 - 1).
Le 1er facteur f1s'annule en (√2 ± √6)/2 dont on retient la valeur positive
(√2 + √6)/2 ≈ 1,93 compte tenu de l'intervalle d'étude. Le
second facteur f2 s'annule en (-√2 ± √6)/2 dont on retient la valeur
positive (-√2 + √6)/2 ≈ 0,52. Le signe des deux trinômes conduisent au
tableau de variation de f :
'(x)
est du signe de (x2 - 1)2 - 2x2 qui se
factorise en (x2 + x√2 - 1)(x2 - x√2 - 1).
Le 1er facteur f1s'annule en (√2 ± √6)/2 dont on retient la valeur positive
(√2 + √6)/2 ≈ 1,93 compte tenu de l'intervalle d'étude. Le
second facteur f2 s'annule en (-√2 ± √6)/2 dont on retient la valeur
positive (-√2 + √6)/2 ≈ 0,52. Le signe des deux trinômes conduisent au
tableau de variation de f :
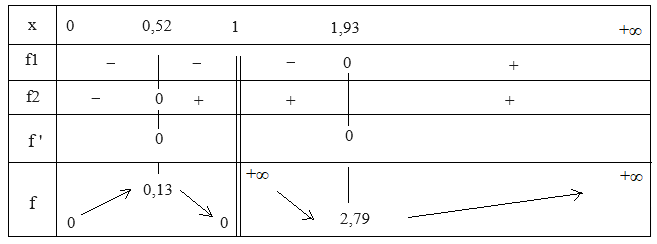
en x = 0, y = 0, la tangente à l'origine a pour coefficient directeur 1/e (en bleu sur le graphique ci-dessous).
en x = (-√2 + √6)/2 ≈ 0,52, f passe par un maximum local (environ 0,13) avec tangente horizontale à la courbe (C)
Pour x infini, le facteur exponentiel de y tend vers e0 = 1. La limite de f est donc infinie.
2°/ Lorsque x tend vers 1 par valeurs supérieures, x2 - 1 tend vers 0 positivement, le facteur exponentiel tend donc vers +∞ et f(x) tend donc également vers +∞. Par imparité la limite de f(x) pour x tendant vers -1 par valeurs inférieures est -∞.
Lorsque x tend vers 1- (x tend vers 1 par valeurs inférieures) : x2 - 1 tend vers 0 par valeurs inférieures, son inverse tend donc vers -∞, c'est dire que le facteur exponentiel de f(x) tend vers 0 : la limite de f est donc nulle. Qu'en est-il de la tangente en ce point d'arrêt ? Revenons à la définition de la dérivée en un point en calculant la limite de :
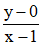
Pour lever l'indétermination, on peut écrire, en posant u = 1/(1 - x2) :
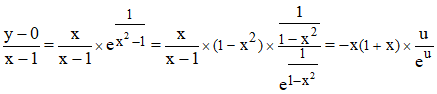
Or u = 1/(1 - x2) tend vers +∞, le rapport u/eu tend donc vers 0 et le produit - x(1 + x) tend vers -2. En conclusion le coefficient directeur de la tangente en x = 1- est nul. La fonction étant impaire, il en est de même lorsque x tend vers -1 par valeurs supérieures. On constate ces résultats sur le graphique ci-dessous
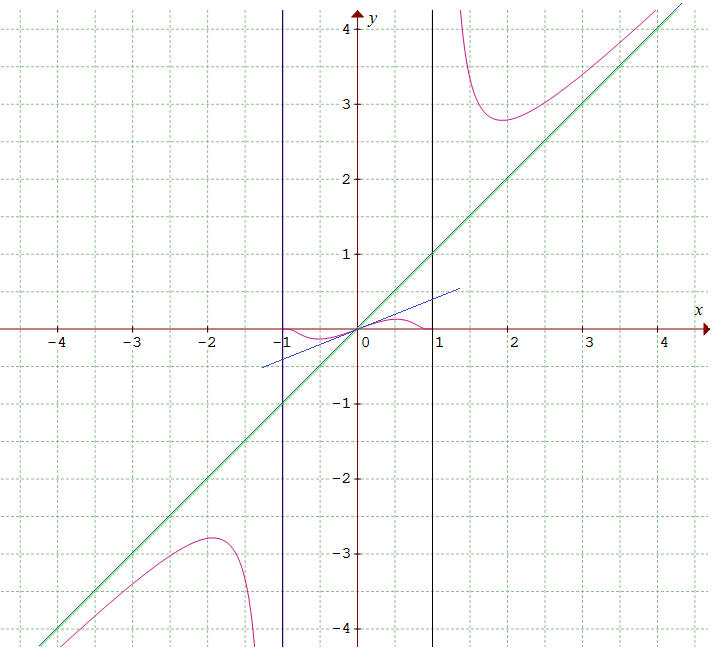
3°/ Lorsque x tend vers l'infini, f(x)/x =e1/(x² - 1) tend vers 1 car 1/(x2 - 1) tend vers 0. La courbe admettra la 1ère bissectrice du repère comme asymptote oblique à condition que f(x) - x tende vers 0 pour x infini.
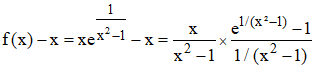
Posons là encore u = 1/(1 - x2) qui, dans ce cas tend vers 0. Le 1er facteur du 3è membre ci-dessus tend vers 0. Étudions (eu - 1)/u.
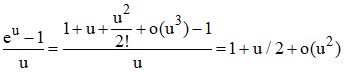
Ce rapport tend donc vers 1, par suite f(x) - x tend vers 0 × 1 = 0 : la courbe (C) admet effectivement la 1ère bissectrice comme asymptote oblique pour infini (en vert ci-dessus).