ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Apprendre à démontrer : translation, milieu & symétrie centrale     niveau 4ème

• Dessine un carré ABCD de côté 4 cm.
• On appelle E le symétrique de D par rapport à A;
• On appelle F le symétrique de C par rapport à B;

  1° - Fais une figure soignée.

    i   Vérifie la figure obtenue en cliquant ici...

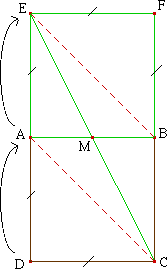
  2° - Trace, sans justification (une fois n'est pas coutume), l'image du carré ABCD par la translation qui transforme C en B.

3° - Trace le segment [EC].

Démontre maintenant que [EC] coupe [AB] en son milieu que tu appelleras M.

1° - Figure :

2° - La translation est une transformation qui conserve le parallélisme, les angles et les distances. L'image d'un carré est un carré. L'image du carré ABCD dans la translation qui transforme C en B est le carré AEFB.

 ➔   Ce résultat montre que dans une translation, il ne faut pas toujours lier l'image d'un point à l'existence d'un parallélogramme.

Le concept de parallélogramme "aplati" utilisé pour des points alignés est également très artificiel ici, car dire que [DE] et [AA] ont même milieu est un peu tiré par les cheveux... En résumé, exiger une explication serait ici mettre les élèves en grand embarras, comme pour tout ce qui leur paraît trop évident. Il faut parfois savoir accepter le "c'est forcé".

3° - Dans la .................. qui transforme C en B, le point ...... a pour image E. Le quadrilatère CBEA possède donc deux ......... parallèles de même .................. C'est donc un ....................... et ses ................. ont alors même milieu. Par conséquent [EC] passe par ....., milieu de [AB].