Angles alternes-internes

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Apprendre à démontrer : angles alternes-internes niveau 5ème

ABC est un triangle (quelconque). On a tracé les bissectrices des angles ^B et ^C.
La parallèle au côté [BC] passant par I coupent les côtés [AB] et [AC] respectivement en D et E.

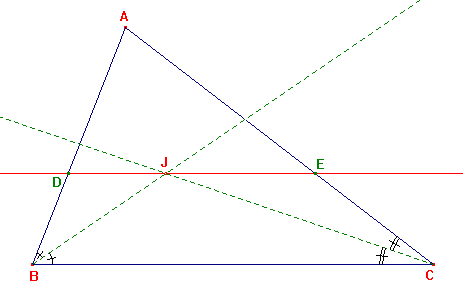
On demande de prouver que DE = DB + EC.

Si tu sèches après avoir bien cherché : ››››

Solution :

Deux droites parallèles (d1) et (d2) coupées par une sécantes (s) déterminent des angles alternes-internes égaux (alternes car ils sont de part et d'autre de la sécante et internes car ils sont à l'intérieur de la bande que forment les parallèles) :

♦ Par hypothèse, les droites (DE) et (BC) sont parallèles, elles déterminent donc avec la sécante (BJ) des angles alternes-internes égaux :

^DBJ = ^DJB

Le triangle DBJ ayant deux angles de même mesure en B et J est donc isocèle, de sommet principal D. Par conséquent :

DJ = DB

♦ On raisonne de même dans le triangle JEC :

JE = EC

♦ Or DE = DJ + JE. Par conséquent :

DE = DB + EC

C.Q.F.D.