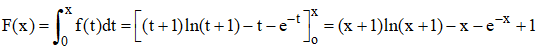ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
Étude de la fonction ln(x + 1) + e-x
niveau TerC/BTS |
» Source : inspirée du sujet BTS Informatique de gestion 1990 (exo III analyse)
1°/ Préliminaire :
a) Étudier le sens de variation de la fonction g définie par :
∀ x ∈ R : g(x) = ex - x - 1
b) Déduire de l'étude précédente que ∀ x ∈ R : ex ≥ x + 1
2°/ Étudier le sens de variation de la fonction f, définie par :
∀ x > - 1 : f(x) = ln(x + 1) + e-x
3°/ a) Préciser les limites de
f aux bornes de son ensemble de définition.
b) Représenter ses variations dans un repère orthonormé
(on choisira 1,5 cm comme unité). On appelle (C) la courbe obtenue.
c) Justifier que (C) est asymptote à la courbe (L)
représentative de x → ln(x + 1) au voisinage de +∞.
4°/ a) Calculer f
'', dérivée seconde de f.
b) Vérifier que f''(x)
est du signe de (x + 1)2 - ex et s'annule en changeant de
signe en x = 0 et en une valeur α proche de 2,5
que l'on précisera à 0,01
près. Quelles interprétations pour
(C) au voisinage de ces points ?
5°/ On sait, ou on admettra,
qu'une primitive de x → lnx,
est x → xlnx
- x. Calculer la primitive nulle en 0 de la fonction f :
Si vous séchez après avoir bien cherché : ››››
| Solution : |
1°/ Préliminaire :
a) Composée de fonctions dérivables sur R, g est dérivable sur R et g'(x) = ex - 1 ≥ 0 ssi x ≥ 0 : g décroît (resp. croît) strictement sur R- (resp. sur R+) et g(0) = 0 (minimum absolu).
b) On déduit de a) que g(x) ≥ 0. C'est dire que g(x) = ex - x - 1 est positif ou nul pour tout x de R, donc que :
∀ x ∈ R : ex ≥ x + 1
2°/ Étude de la fonction f, posons J = ]-1, +∞[ :
Composée de fonctions dérivables sur J, f est dérivable sur cet intervalle et :
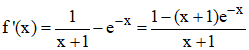
Multiplions le 3è membre ci-dessus, haut et bas, par ex :
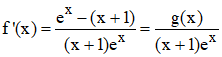
x + 1 étant positif sur J, f'(x)
est du signe de g(x), c'est à dire positive, nulle en x = 0. La fonction f
est strictement croissante sur J et sa courbe admet en x = 0 une tangente
horizontale (parallèle à l'axe des abscisses).
3°/ a) Lorsque x tend vers -1, e-x
tend vers e et, x + 1 tendant vers 0+, ln(x + 1) tend vers -∞;
par suite f tend vers -∞.
b) Lorsque x tend vers +∞, ln(x + 1) tend vers +∞, et e-x
= 1/ex tend vers 0 : f tend vers +∞.
c) Lorsque x tend vers +∞, f(x) - ln(x + 1) = e-x
= 1/ex tend vers 0 : les deux courbes se confondent donc à
l'infini : elles sont asymptotes l'une de l'autre.
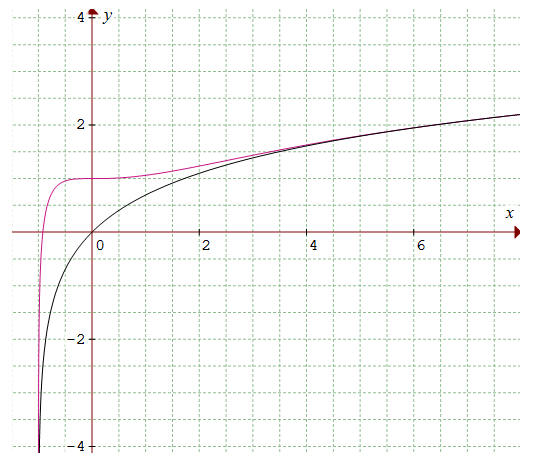
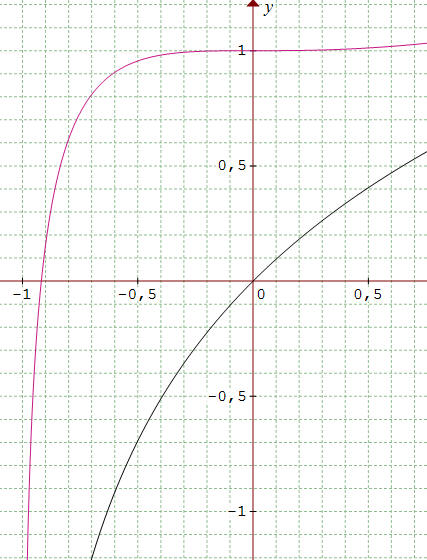
➔ Au voisinage de x = -1, il en va autrement puisque f(x) - ln(x + 1) = e-x tend vers e, ce qui n'apparaît pas clairement sur le graphique ci-dessus eu égard à l'échelle. En zoomant, on se rend mieux compte de la situation. Par exemple en x = - 0,7, f(x) - ln(x + 1) vaut graphiquement sensiblement 2, c'est à dire e0,7.
4°/ a) Calculons f''(x)
:
b) Multiplions f''(x)
par ex > 0 pour tout x :
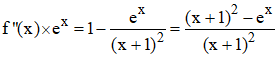
f"(x)
est donc du signe de (x + 1)2
- ex.
b) Traçons la parabole x → (x + 1)2 et la courbe x → ex sur l'intervalle ]-1, +∞[. Les deux courbes se "croisent" en x = 0 et x = α avec α ≈ 2,5.
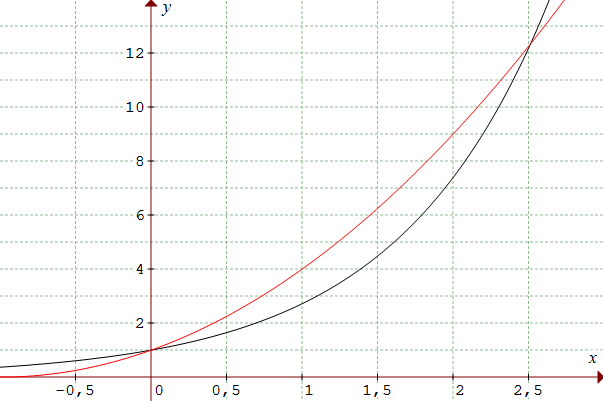
en noir y = ex, en rouge l'arc de parabole y = (x+1)2
♦ Au voisinage de x = 0 :
Pour x < 0, l'arc de parabole est
"au-dessous" de la courbe exponentielle, f"(x)
est donc négative.
Pour x > 0, l'arc de parabole est
"au-dessus" de la courbe exponentielle, f"(x)
est donc positive.
➔ Graphiquement, (C) présente un point d'inflexion : elle change de concavité (concave → convexe).
♦ Au voisinage de α = 2,5 :
Précisons cette valeur approchée :
(2,5 + 1)2
- e2,5 ≈ 0,0675 > 0; (2,51 + 1)2
- e2,51 ≈ 0,0151 > 0;
(2,52 + 1)2
- e2,52 ≈ - 0,0381 < 0;
On peut donc affirmer 2,51 < α < 2,52.
Pour x < α, l'arc de parabole est
"au-dessus" de la courbe exponentielle, f"(x)
est donc positive.
Pour x > α, l'arc de parabole est
"au-dessous" de la courbe exponentielle, f"(x)
est donc négative.
➔ Graphiquement, (C) présente un second point d'inflexion : elle change de concavité (convexe → concave).
5°/ Une primitive de ∫ln(x + 1)dx est ∫ln(x + 1)d(x+1) = (x + 1)ln(x + 1) - (x + 1), soit (x + 1)ln(x + 1) - x à une constante additive près. Une primitive de x → e-x est x → - e-x. Par suite :
