ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

SOBOLEV Sergueï Lvovitch, russe, 1908-1989

Sergueï Sobolev fut un des grands mathématiciens et physiciens atomiques russes de l'époque soviétique (URSS). Il étudia à Saint-Pétersbourg, ancienne capitale des tsars, rebaptisée Leningrad après la révolution bolchévique de 1917. Sa thèse de doctorat (1929), portant sur l'étude des systèmes d'équations aux dérivées partielles, orienta sa carrière. Professeur à l'université Lomonosov de Moscou, il dirigea également l'Institut de mathématiques de l'université de Novossibirsk (Sibérie) mise en place en 1959.

Spécialiste en équations différentielles appliquées aux sciences physiques, Sobolev introduit, dès 1934, la notion de dérivée généralisée également dite faible, afin de mieux appréhender les phénomènes physiques.

Le concept de fonction, initiée par Leibniz, s'avérait insuffisant dans la recherche des solutions d'équations aux dérivées partielles (comme le problème de Dirichlet) : il est ainsi à l'origine de la théorie des distributions développée par son compatriote Israël Guelfand et le français Laurent Schwartz.

Soit J un intervalle ouvert de R (non nécessairement borné) et f une fonction de carré intégrable sur J, élément de L²(J).
On suppose qu'il existe φ de carré intégrable sur J telle que  :

             » espaces L^p

où a est un réel donné de J. On dit que φ est la dérivée faible de f sur J. Dans ces conditions, φ est unique, f est continue et sera constante ssi φ est nulle (ces propriétés s'entendent presque partout).

 ➔  Noter que si φ est continue, f apparaît comme la primitive de φ nulle en x = a et φ est une dérivée au sens usuel.

• Dans les hypothèses de la définition, l'inégalité de Hölder (équivalente ici à celle de Cauchy-Schwarz) assure l'existence de l'intégrale de φ × 1_[a,x] sur l'intervalle [a,x].

• L'inégalité de  Cauchy-Schwarz) appliquée à |f(x_o + h) - f(x_o)|, module de l'intégrale de φ × 1_{[xo , xo+h]} sur l'intervalle [x_o , x_o + h] assure la continuité de f.

• La nullité de φ pour f constante est plus subtile : si f est constante, on a f(x) = f(x') pour tous x et x' de J. Par suite, l'intégrale de φ sur [x,x'] est nulle et elle peut s'écrire dans l'espace de Hilbert L²(J) :

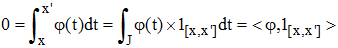
φ est donc orthogonale à toute fonction en escalier de J; or l'ensemble de ces fonctions est dense dans L²(J). Dans cet espace métrique engendré par sa norme ||  ||₂, on peut écrire qu'il existe une suite (e_n) de fonctions en escalier tendant vers φ au sens de ||  ||₂ :

0 = lim  || φ - e_n ||₂² = lim ( || φ ||₂² + || e_n ||₂² - 2<φ ,e_n >) = lim ( || φ ||₂² + || e_n ||₂²)

 || φ ||₂ est donc nécessairement nul, donc (la classe de) φ est nulle.

Un ensemble de Sobolev dans L^p(J) est un ensemble de fonctions de L^p(J) admettant une dérivée faible dans cet espace.

 ➔   Pour en savoir plus :

1. Espaces de Sobolev, par Pierre Bérard, Institut Fourier
   https://www-fourier.ujf-grenoble.fr/~pberard/E/MEDP-0102/medp-sobolev.pdf

2. Espaces de Sobolev : http://www.univ-orleans.fr/mapmo/membres/maitine/MASTER1/probleme.pdf,
   page de Maïtine Bergounioux (professeur Univ. Orléans).

3. Méthodes mathématiques pour les sciences physiques (niveau master), par Laurent Schwartz, Ed. Hermann, Paris, 1965

4. Intégration & Analyse hilbertienne, A. Guichardet , Éd. Ellipses X École polytechnique, Paris, 1989

---

Pontriaguine  Chevalley

---

© Serge Mehl - www.chronomath.com