ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 Né
à Saint-Affrique (Aveyron), Pierre Sarrus commença des études médecine qu'il
abandonne au profit d'études de Mathématiques à Montpellier.
Né
à Saint-Affrique (Aveyron), Pierre Sarrus commença des études médecine qu'il
abandonne au profit d'études de Mathématiques à Montpellier.
Après son doctorat et l'agrégation de mathématiques, il sera professeur de sciences physiques à Perpignan (1827). Deux ans plus tard, il est nommé professeur à la faculté des sciences de Strasbourg. Sarrus en sera le doyen en 1831 et recevra (1848) le prix de l'Académie des sciences pour son application aux intégrales multiples du calcul des variations dans la recherche d'extrema.
Outre des travaux en astronomie, Pierre Sarrus est principalement connu aujourd'hui pour sa célèbre règle et ses travaux en algèbre linéaire (systèmes d'équations linéaires) parallèlement à ceux de Cayley et Hamilton.
» Source image et éléments de biographie : avec l'aimable autorisation du Portail de la ville de Saint-Affrique en Aveyron où l'on trouvera une biographie plus complète en cliquant sur l'image.
| Règle de Sarrus : |
Il s'agit d'un procédé rapide de calcul d'un
déterminant d'ordre 3. Connaissant le développement suivant la 1ère
colonne :
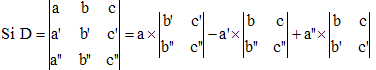
d’où :
D = ab'c" - ab"c' - a'bc" + a'b"c + a"bc' - a"b'c = ab'c" + bc'a" + ca'b" - a"b'c - b"c'a - c"a'b
|
Procédé mnémotechnique : |
Posons D = ab'c" + bc'a" + ca'b" - (a"b'c + b"c'a + c"a'b) = p1 + p2 + p3 - (p4 + p5 + p6)
On écrit à droite du déterminant les deux premières colonnes.
Pour obtenir la valeur de D, on somme les produits des trois termes diagonaux "descendants" p1 + p2 + p3, comme indiqué ci-contre, à laquelle on soustrait la somme p4 + p5 + p6 obtenue avec les trois termes diagonaux "ascendants".