ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 ROBERVAL Gilles de-,
français, 1602-1675 |
Natif
de Roberval, village près de Beauvais, Gilles Personier,
aujourd'hui souvent nommé Gilles Personne, fut un personnage
éclectique et passionné, tant par la philosophie que par
les sciences. Autodidacte et démuni, vivant de leçons particulières, il
"monte" à Paris (1627) et se lie d'amitié avec
l'abbé Mersenne et Etienne
Pascal, entrant ainsi dans le cénacle de la pensée scientifique de l'époque.
Roberval enseigna la philosophie au collège Gervais (1631) puis fut nommé professeur de mathématiques au Collège Royal de France. Il sera un des membres fondateurs de l'Académie des Sciences (1665).
On lui doit la balance (1670) qui porte son nom, dont le fonctionnement fut publié dans le Journal des Savants sous le titre : Une nouvelle manière de balance inventée par M. de Roberval, professeur de mathématiques dans l'université de Paris.
Étude géométrique du principe de la balance de Roberval : »
| Calcul différentiel, quadratures, tangente aux courbes : |
Admirateur d'Archimède,
il se distingua par des travaux sur l'application
à la géométrie de la méthode des indivisibles de Cavalieri,
proche du calcul intégral, tout en revendiquant la paternité
de ladite méthode pour avoir utilisé auparavant le même principe dans le calcul de l'aire de la
parabole (1636). Quoi qu'il en soit, il put ainsi déterminer des aires (quadratures),
comme celle du cône droit ou oblique,
et des volumes engendrés par diverses courbes comme la
parabole
ou l'hyperbole.
Étudiant le paradoxe des deux roues
d'Aristote,
il sera le premier amené à étudier ("inventer")
la sinusoïde,
la strophoïde, qu'il appela alors
ptéroïde et la
cycloïde
déjà remarquée par Galilée qui s'intéressait à la
mesure de ses arches. Il s'agit là d'un cas particulier de trochoïde, que Pascal
appela
roulette.
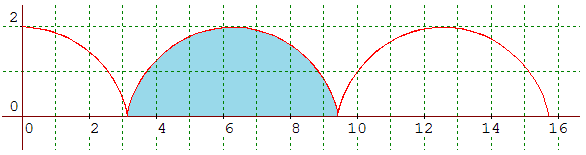
Répondant à une demande de son ami Mersenne, il réussit à calculer (1638), au moyen de la méthode des indivisibles, l'aire délimitée par une arche de cycloïde, à savoir 3πr2 si r désigne le rayon du cercle roulant. La longueur de l'arche est alors 8r. Un résultat que retrouva Torricelli en 1644 et qui fut la source de correspondances enflammées en termes de reconnaissance de paternité...
On doit aussi à Roberval, indépendamment de Torricelli, les premiers travaux concernant la recherche des tangentes aux courbes planes (on disait à l'époque les touchantes), ce qui le brouilla gravement avec Descartes...
Étude générale des trochoïdes : »
➔ Pour en savoir plus :
Dans le cadre des célébrations nationales,
page du ministère de la culture (2002)
pour le 400è anniversaire
de la naissance de Roberval :
http://www.culture.gouv.fr/culture/actualites/celebrations2002/roberval.htm
Torricelli