ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
MERTENS Franz,
allemand
d'origine polonaise, 1840-1927 |
Né à Posen, à l'époque en Prusse de 1815 à
1848, aujourd'hui Środa en Pologne, Mertens
étudia les mathématiques à Berlin où Weierstrass fut un de ses professeurs. Il
obtint son doctorat en 1865 portant sur la
théorie du potentiel sous la direction de
Kummer et Kronecker.
Il enseigna à Graz et à Vienne.
Son nom nous est particulièrement familier de par son théorème sur les séries produits complétant celui de Cauchy et des résultats concernant la distribution des nombres premiers.
|
Théorème de Mertens sur les séries produits (1875) : |
Lorsque les séries numériques Σun et Σvn sont convergentes, l'une au moins étant absolument convergente, alors, en notant vers u et v leurs sommes respectives, la série produit, définie ci-dessous, de terme général wn , est également convergente et sa somme est le produit uv.
wn = Σukvn-k = uovn + u1vn-1 + u2vn-2 + ... unvo
En savoir plus sur les séries et leur convergence : »
|
Théorèmes de Mertens relatifs à la distribution des nombres premiers (1874) : |
n désignant un entier naturel (non nul) et ln la fonction logarithme népérien :
»
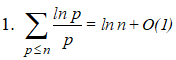
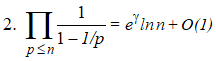
Distribution des nombres premiers : » Produit eulérien : »
➔ Pour en savoir plus :
Les séries mathématiques, par Gaston Casanova, Que sais-je ? n°1567. P.U.F, Paris - 1974
L'Analyse au fil de l'histoire
Ce livre est partiellement en ligne sur Google Livres à
cette adresse.
Les Nombres premiers, par Gérald Tenenbaum, Michel Mendès-France, Que Sais-je n°571, Ed. PUF - 1997
Sur un théorème de Mertens, par Olivier Ramaré
(CNRS) :
Cornu