ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

On appelle généralement ainsi les cubiques d'équation :
Cette appellation provient de la présence de trois branches infinies (les trois dents, en quelque sorte) opposées à une quatrième constituant le manche... Ces courbes furent étudiées par Newton et Descartes dans le cadre d'une classification typologique des courbes algébriques.
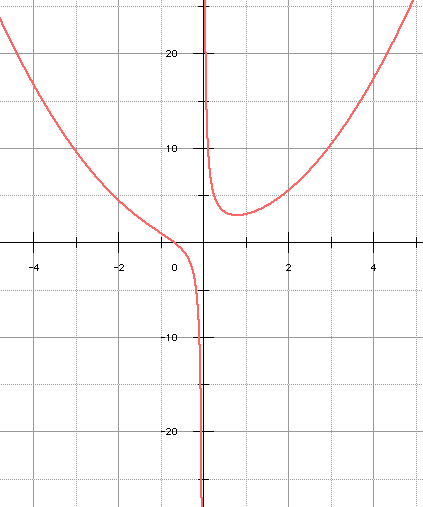
xy = x3 + x + 1
| Parabole asymptote : |
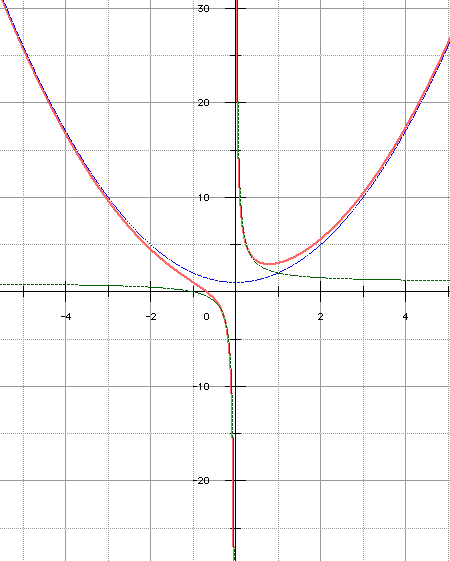
Écrite sous la forme y = ax2 + bx + c + d/x, l'équation du trident montre qu'au voisinage de l'infini, la courbe est asymptote à la parabole d'équation y = ax2 + bx + c car d/x tend vers 0. A contrario, au voisinage de 0, l'hyperbole d'équation y = c + d/x est asymptote à la courbe car ax2 + bx tend vers 0 :
| Étude de différents cas : |
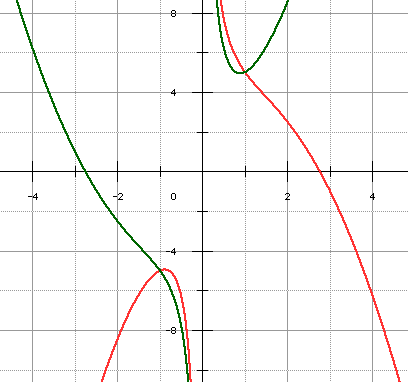
On remarquera que par le jeu de de symétries par rapport aux axes, les différents cas peuvent se réduire à a > 0 et d > 0. Par exemple, si nous voulions étudier le cas y = -x2 + 2x + 1 + 3/x, le changement de y en -y et de x en - x, conduit à étudier y = x2 + 2x - 1 + 3/x : on obtiendra une courbe symétrique par rapport à l'origine :
| Étude au moyen de la fonction dérivée : |
Sous la forme cartésienne, la fonction dérivée est :
y' = 2ax + b - d/x2
Le signe de y' peut être étudié en recherchant l'intersection de la droite d'équation y = 2ax + b et de la courbe y = d/x2. Suivant la valeur de d en fonction de a et b, y' admet 1, 2 ou 3 zéros :
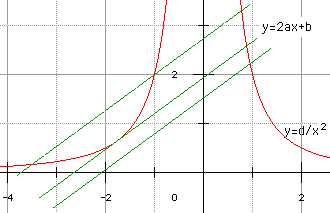
Le cas d = b3/27a2 correspond à un zéro double (et un zéro simple) pour y'. Nous étudions ci-après trois cas particuliers :
♦ y = x2 + 3x + 1 + 1/x , y' admet un zéro double et un zéro simple (inflexion en x = -1) :
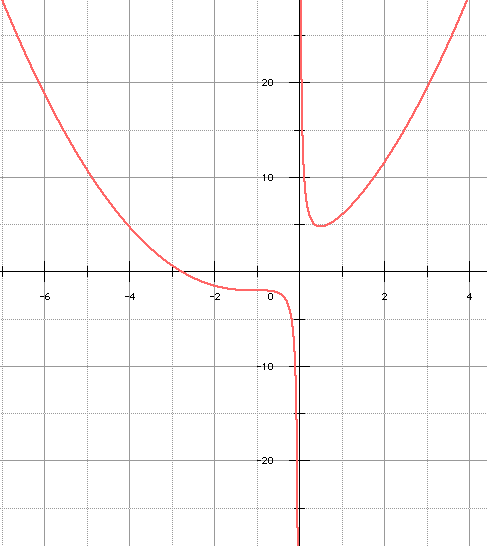
♦ y = x2 + 2x + 1 + 1/x , y' n'admet qu'un seul zéro :
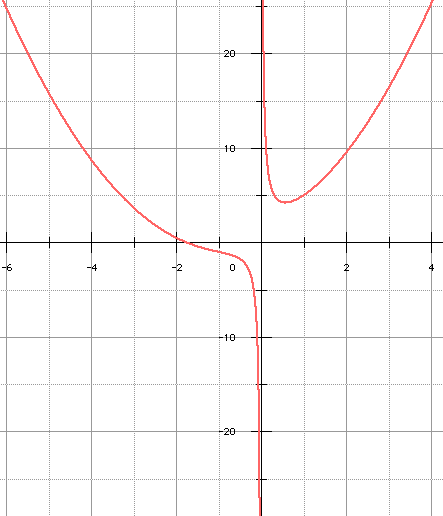
♦ y = x2 + 4x + 1 + 1/x , y' admet 3 zéros simples :