ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Triangle arithmétique
également appelé
triangle de Pascal |
La notation Cnp désigne le nombre de parties de cardinal p dans un ensemble de cardinal n. Autrement dit, Cnp est le nombre façons de choisir p éléments parmi n éléments distincts (0 ≤ p ≤ n), aucun ordre n'intervenant dans ce choix. Noter que choisir p éléments, c'est choisir de ne pas choisir les n - p restants... : Cnp = Cnn-p. On a la formule :
On peut aisément calculer les combinaisons Cnp en vertu de la formule de récurrence :
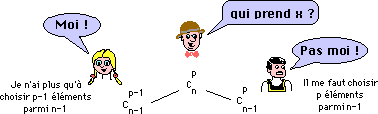
Le schéma ci-dessous justifie la formule de récurrence énoncée :
| Programmation sur Tableur : |
L'ordinateur, et plus précisément le tableur, est très à l'aise pour traiter ce petit problème d'arithmétique. Le mode L1C1 d'EXCEL est ici utilisé : la colonne1 porte les valeurs de n et la ligne 1 les valeurs de p.
En L2C1, on inscrit 0, puis en L3C1, la formule : = L(-1)C + 1, que l'on recopie vers le bas autant que voulu;
En L1C2, on inscrit 0, puis en L1C3, la formule : = LC(-1) + 1 et on recopie vers la droite (autant de fois que pour n).
En L2C2, on a inscrit la formule (magique) de récurrence :
=SI(L1=0;1;SI(COLONNE()>LIGNE();"";SI(COLONNE()=LIGNE();1;L(-1)C(-1)+L(-1)C)))
qui est recopiée vers le bas puis, en bloc, vers la droite.
Résultat d'exécution :
|
n\p |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0 |
1 |
||||||||||||||
|
1 |
1 |
1 |
|||||||||||||
|
2 |
1 |
2 |
1 |
||||||||||||
|
3 |
1 |
3 |
3 |
1 |
|||||||||||
|
4 |
1 |
4 |
6 |
4 |
1 |
||||||||||
|
5 |
1 |
5 |
10 |
10 |
5 |
1 |
|||||||||
|
6 |
1 |
6 |
15 |
20 |
15 |
6 |
1 |
||||||||
|
7 |
1 |
7 |
21 |
35 |
35 |
21 |
7 |
1 |
|||||||
|
8 |
1 |
8 |
28 |
56 |
70 |
56 |
28 |
8 |
1 |
||||||
|
9 |
1 |
9 |
36 |
84 |
126 |
126 |
84 |
36 |
9 |
1 |
|||||
|
10 |
1 |
10 |
45 |
120 |
210 |
252 |
210 |
120 |
45 |
10 |
1 |
||||
|
11 |
1 |
11 |
55 |
165 |
330 |
462 |
462 |
330 |
165 |
55 |
11 |
1 |
|||
|
12 |
1 |
12 |
66 |
220 |
495 |
792 |
924 |
792 |
495 |
220 |
66 |
12 |
1 |
||
|
13 |
1 |
13 |
78 |
286 |
715 |
1287 |
1716 |
1716 |
1287 |
715 |
286 |
78 |
13 |
1 |
|
|
14 |
1 |
14 |
91 |
364 |
1001 |
2002 |
3003 |
3432 |
3003 |
2002 |
1001 |
364 |
91 |
14 |
1 |
Par exemple, C94= 126 : il y a 126 choix de 4 objets parmi 9.
∗∗∗ Exercices
On tire 5 cartes au hasard dans un jeu de 32.
On note la "donne" obtenue. On replace les cartes dans le jeu, on mélange. On
retire 5 cartes. En admettant que les donnes soient équiprobables (même
probabilité d'apparition) au 1er et second tirage (faux dans la pratique),
quelle est la probabilité de "retomber" sur les mêmes cartes ?
On a là 1
chance sur 201376 car le nombre de donnes possibles est :
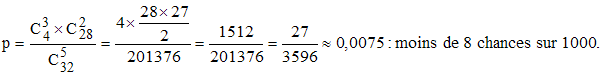
Loi hypergéométrique : »