
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

 |
|
Un segment [AB] de longueur constante se déplace sur le demi-cercle. On note I le milieu de [AB]. A et B se projettent orthogonalement en A' et B' sur le diamètre. Que peut-on dire du triangle IA'B' ?
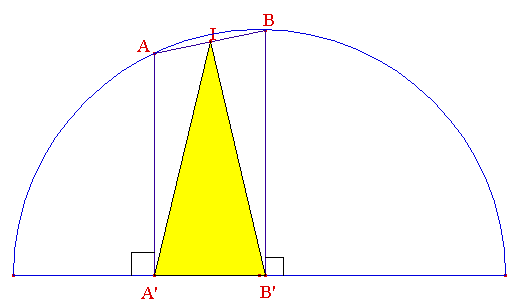
La figure dynamique ci-dessous est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet :

Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Tu peux déplacer le point A sur le
demi-cercle
Si tu sèches après avoir bien cherché : »
| Solution : |
On conjecture (conjecturer = penser, présumer) que le triangle A'IB' reste isocèle et, mieux, qu'il reste semblable à lui même : ses angles sont constants. Montrons cela !
Rétablissons quelque peu la symétrie en traçant le cercle entier et en plaçant les symétriques A" et B" de A et B par rapport au diamètre (A'B') :
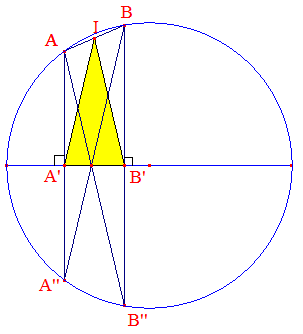

• I est le milieu de [AB], A' est celui de [AA"], B' celui de [BB"];
• Dans les triangles ABA" et ABB" on a respectivement IA' = A"B/2 et IB' = AB"/2 (en application de la droite des milieux, ou de la propriété de Thalès);
• Dans la symétrie d'axe (A'B'), [AB"] a pour image [A"B], donc A"B = AB".
Le triangle A'IB' est donc isocèle.
• [AB] gardant une mesure constante, il en est de même de l'arc AB et en tant qu'angle inscrit interceptant un tel arc, l'angle ^AB"B garde une mesure constante. Or ^AB"B = ^IB'B : angles correspondants formés par les parallèles (IB') et (AB") coupées par la sécante (BB').
Par suite, ^IB'A' garde une mesure constante. Il est clair qu'un triangle isocèle dont un des angles est invariant (en mesure) voit ses deux autres angles posséder cette même propriété.