ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Trajectoires orthogonales d'une courbe ou d'une familles de courbes planes

L'étude générale de ce sujet vit le jour au 18è siècle, lancé comme un défi par Jean Bernoulli et Leibniz au mathématiciens européens dans le but de prouver l'efficacité du concept de de différentielle comparé au calcul des fluxions de Newton. Ce sera Stirling, adepte des méthodes newtoniennes, qui en donna le premier une solution générale en 1715 !

La Terre étant assimilée à une sphère, un exemple élémentaire de trajectoires orthogonales dans l'espace est celui des parallèles (définissant la latitude) qui rencontrent perpendiculairement tout méridien (définissant la longitude et les fuseaux horaires).

» Mercator , Loxodromie

Restons dans le cas du plan et commençons par un cas élémentaire purement géométrique :

Trajectoires orthogonales d'un cercle du plan :    

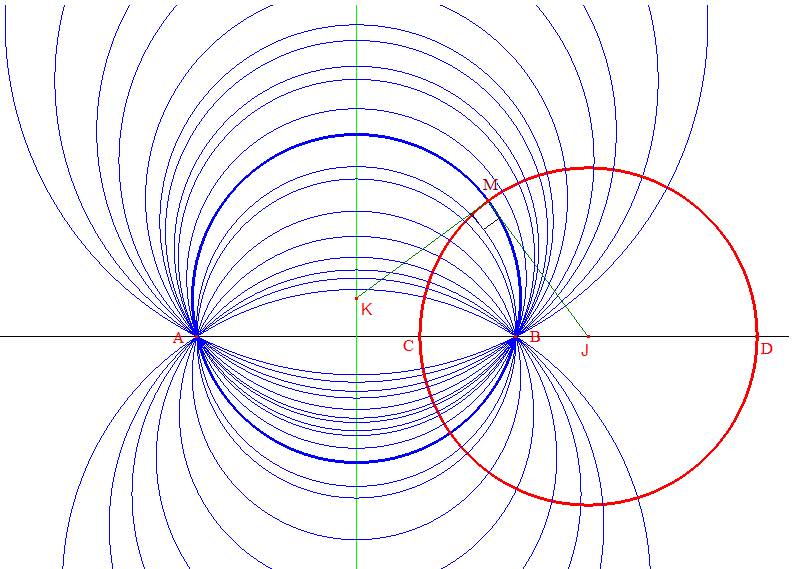
Deux cercles sont dits orthogonaux si les tangentes en leur(s) point(s) d'intersection sont perpendiculaires. Considérons alors une droite (ACD) et B le point de cette droite tel que la division[ABCD] soit harmonique. Rappelons alors ce résultat :

Deux cercles sont orthogonaux si et seulement si le diamètre de l'un est divisé harmoniquement par l'autre

Considérons alors l'ensemble des cercles passant par A et B. Ces cercles sont centrés sur la médiatrice de [AB] et constituent l'ensemble des trajectoires orthogonales au cercle de diamètre [CD].

Ci-dessus, on a privilégié un cercle de centre K, élément de l'ensemble des cercles orthogonaux au cercle donné de centre J.
La division [A,B,C,D] est harmonique. On a (KM)  ⊥ (JM).

Développante et trajectoires orthogonales des tangentes :  »       Tractrice :  »

Cas général d'une famille de courbes définie par une équation cartésienne :     

Dans un repère orthonormé du plan, soit Φ une famille de courbes planes définie par l'équation :

f(x,y,a) = 0, (x,y)∈U        (1)

où a désigne un paramètre réel et U un domaine de R² (partie ouverte et connexe). On suppose f continument différentiable sur U, c'est à dire que ses dérivées partielles par rapport à x et y existent et sont continues sur U.

L'ensemble 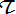des courbes qui coupent à angle droit toutes les courbes de Φ constitue l'ensemble des trajectoires orthogonales Φ. Autrement dit, si M(x,y) est un point commun à Φ et 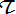, les tangentes en M sont perpendiculaires. On peut renverser cette propriété : Φ est l'ensemble des trajectoires orthogonales de .

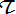On sait que deux droites sont perpendiculaires lorsque le produit de leur coefficient directeur est égal à -1. D'où la méthode :

Par différentiation de (1), on obtient :

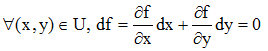
que nous écrivons, pour simplifier l'écriture par la suite :

La tangente en M en tant que point de Φ a pour coefficient directeur :

 Par suite, la tangente en M(x,y) en tant que point de devra avoir pour coefficient directeur :

          (2)

 !  Dans la pratique, il y a là deux conditions f'_x ≠ 0 et f'_y ≠ 0 (gradient non nul) qu'il s'agira de discuter en fin d'étude.

Ces conditions étant posées, une trajectoire (T) de 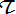doit vérifier les relations (1) et (2) pour toute valeur du paramètre a. Nous devons donc éliminer a entre (1) et (2) :

M(x,y)∈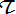 ⇒ f(x,y,a) = 0  et f'_ydx = f'_xdy        (3)

On est en présence d'une équation différentielle du 1er ordre et comme nous avons procédé par conditions nécessaires, on devra à l'issue de la résolution vérifier le bien-fondé de la solution trouvée qui constituera une famille de courbes dépendant d'un paramètre réel k qui n'est autre que la constante d'intégration.

Exemple 1 :  

Quelles sont les trajectoires orthogonales de la famille de paraboles d'équation y = ax² ?

Pour tout (x,y), on a ici U = R² et f(x,y,a) = y - ax² = 0 . f'_{x =} -2ax= 1. On a donc, en appliquant (3) :

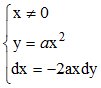
Ce qui conduit à 2ydy = -xdx, soit :

x² + 2y² = k, k∈R⁺

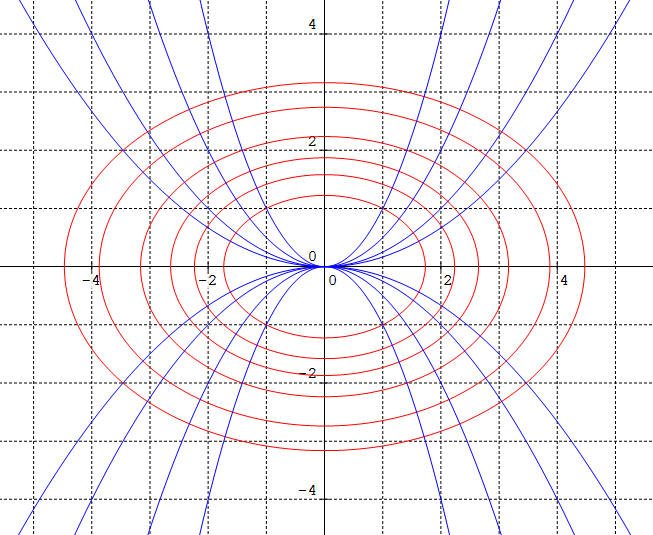
Il s'agit d'une famille d'ellipses. La condition x non nul n'est pas restrictive : à l'exception de k = 0 (ellipse dégénérée) aucune parabole de Φ ne peut rencontrer une ellipse de :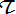

Exemple 2 :  

Recherchons les trajectoires orthogonales de la famille d'ellipses de foyers donnés F'(-c,0) et F(c,0) d'équation

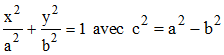        (4)

F et F' étant donnés, la famille d'ellipses ne dépend que du paramètre a > b (axe focal porté par Ox). Différentions et appliquons la relation 3 en remarquant que l'on peut remplacer b² par a² - c² :

On déduit de la seconde équation (différentielle) :

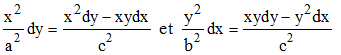
On reporte dans l'équation (1) initiale, ce qui fournit :

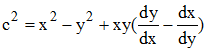
Cela ne semble donc pas simple... Mais remarquons que si nous changeons dy/dx (coefficient directeur des tangentes) en son opposé -dx/dy, l'équation différentielle ci-dessus est inchangée : c'est dire, d'après l'étude précédente que la famille d'ellipses coïncide avec ses trajectoires orthogonales ! Comment-est-ce possible ?

Tout simplement en jouant sur le signe de a² - b² : si b > a, le nombre a² - b² devient négatif. Les foyers étant donnés, on ne peut envisager des ellipses de grand axe situé sur (Oy). Or,  l'équation (4) de la famille peut s'écrire :

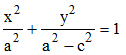
Ce qui signifie que si la restriction a > b n'est plus vérifiée, les calculs restent inchangés et, quitte à poser dans ce cas, a² - c² = - b², on obtiendra la famille d'hyperboles de foyers F' et F, définie par :

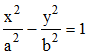
Chaque famille constitue finalement les trajectoires orthogonales de l'autre :

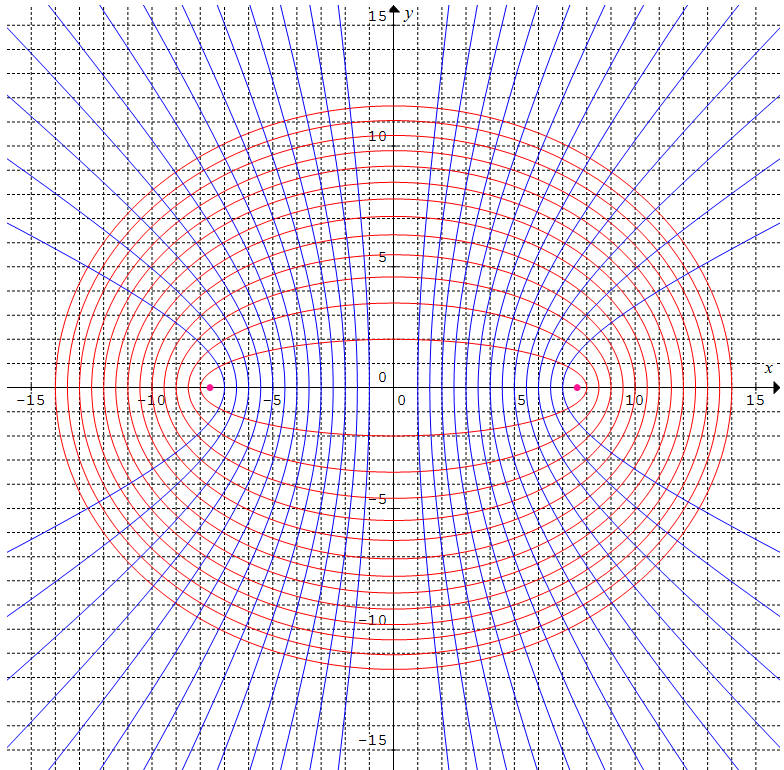
La famille d'ellipses est en rouge, c² = 60. Le paramètre varie de -10 à 10 par pas de 0,5.

∗∗∗
Autre exemple de trajectoires orthogonales d'une famille d'ellipses

Cas général d'une famille de courbes définie par une équation polaire :     

Soit maintenant Φ une famille de courbes planes, a désignant un paramètre réel, définie par l'équation en coordonnées polaires :

r = f(θ,a)   ou plus généralement : f(r,θ,a) = 0        (5)

On procède comme dans le cas des coordonnées cartésiennes : en dérivant par rapport à θ, on obtiendra une équation de la forme :

h(r,r',θ,a) = 0        (6)

avec r' = dr/dθ et tanΦ = r/r' où Φ désigne l'angle de droites ^(OM,T) entre le rayon vecteur et la tangente (» tangente en coordonnées polaires).

Les équations (5) et (6) caractérisent Φ et l'ensemble de ses tangentes (T). Afin de caractériser 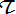et ses tangentes perpendiculaires à (T) en chaque point M de Φ, on conserve (5) et on remplace ^(OM,T) par ^(OM),T) + π/2, donc tanΦ par tan(Φ + π/2), c'est à dire tan Φ par -1/tan Φ = - r'/r.

Autrement dit, dans (6), on devra remplacer :

• r/r' par -r'/r

• ou bien r'/r par -r/r'

• ou encore r' par -r²/r'

Exemple 4 :   

Quelles sont les trajectoires orthogonales de la familles de courbes définie par l'équation polaire r = a.e^t ?

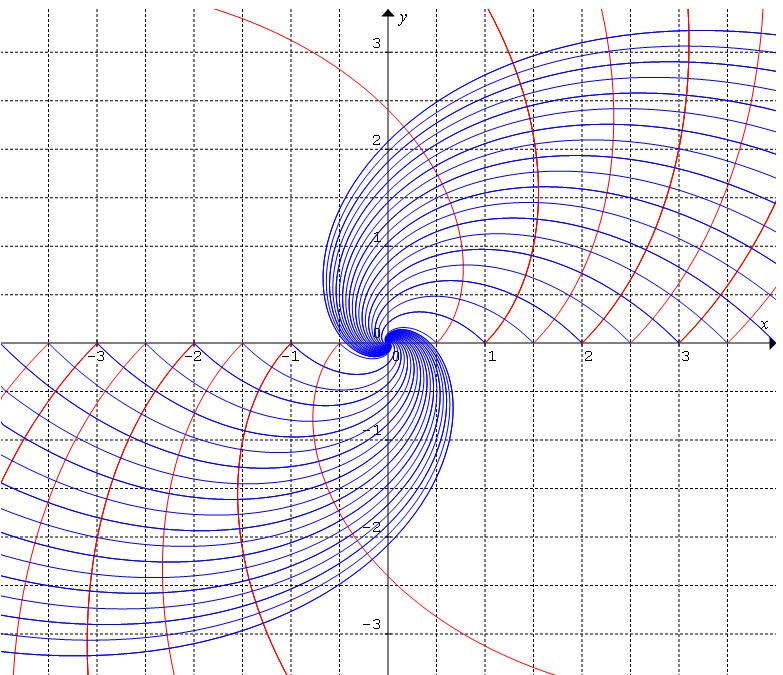
On a r' = a.e^t. Selon la règle ci-dessus 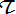est définie par r = a.e^t et -r²/r' = a.e^t. Le paramètre s'élimine immédiatement : on obtient -r/r' = 1, soit r'/r = -1, équation différentielle élémentaire dont la solution est r = ke^-t :

 
La famille r = a.e^t  est en rouge. Le paramètre varie de -10 à 10 par pas de 0,5.

Dans un repère orthonormé, considérons une surface algébrique  S dont l'équation f(x,y,z) = 0 est de la forme polynomiale en x, y et z. On appelle lignes (ou courbes) de niveau de cette surface, l'ensemble des courbes (C_a) définies par f(x,y,a) = 0, c'est à dire les intersections de S avec les plans z = c parallèles au plan (xOy).

Concrètement, ou presque, elles apparaissent par exemple sur les cartes de randonnées de l'IGN (Institut géographique national), ainsi que sur les cartes d'état-major (à usage militaire) des années 1920 pour donner une idée précise des reliefs. Au 19è siècle, on faisait usage de hachures faisant apparaitre les lignes de plus grande pente qui n'étaient autres que les trajectoires orthogonales des lignes de niveau indiquées par des changement de couleur :

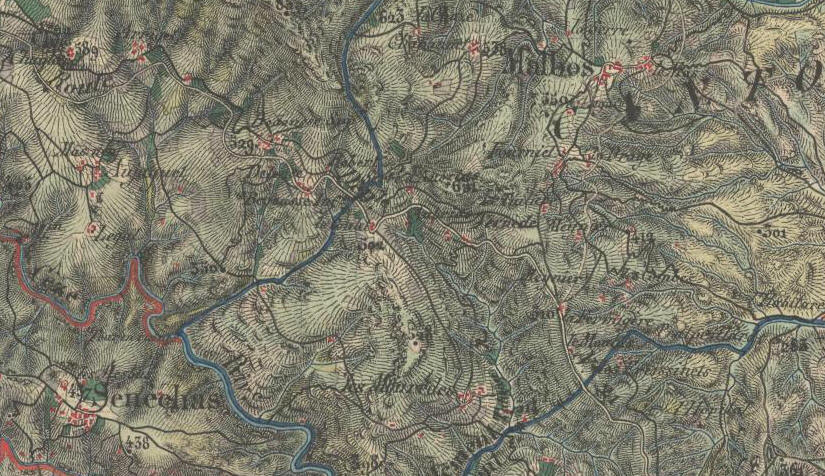
Carte d'état-major (hachurage, 1820) : source IGN

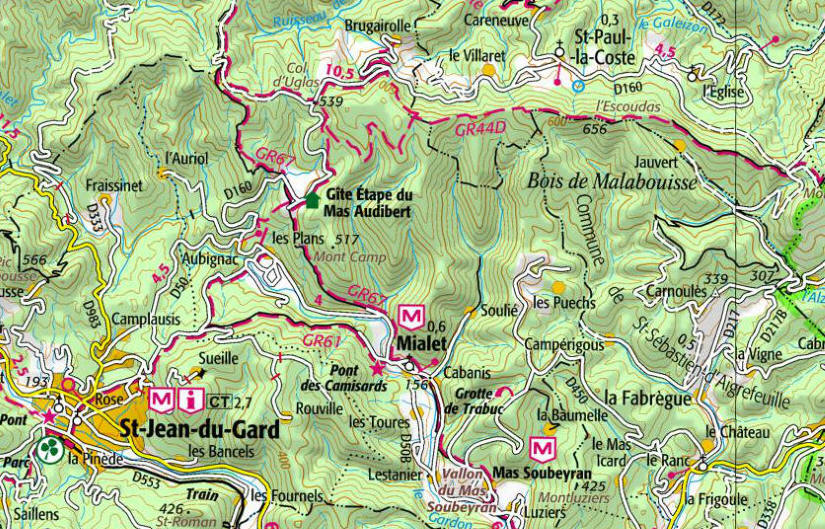
Carte de randonnée 2015 (lignes de niveau) : source IGN

 ➔   On retrouve les lignes de niveau et les trajectoires orthogonales en sciences physiques (potentiel électrostatique ou gravitationnel), respectivement lignes équipotentielles et lignes de forces.