
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
à 28 ans, dans ses Leçons sur la théorie des fonctions (» ref.1), Borel, après des considérations préliminaires relatives (Ch. 1 à 3) :
aux ensembles infinis, la non dénombrabilité de l'intervalle [0,1] de la droite réelle, la puissance du continu;
aux nombres algébriques et transcendants et l'approximation des nombres irrationnels (en particulier au moyen de développements en fraction continue);
aux ensembles dérivés et parfaits selon Cantor et relativement parfait selon Jordan (ensembles contenant leur dérivé, ne différant que d'une partie dénombrable);
définit la mesure de sous-ensembles de l'intervalle [0,1] de R (Ch. 4, page 46 du livre | » ref.1 page 60 du fichier pdf). Lebesgue qualifiera de mesurable B ( B comme Borel) un ensemble mesurable au sens de Borel :


On pourra consulter la totalité de l'ouvrage en réf. 1.
| σ-algèbre (tribu), partie mesurable d'un espace topologique, application mesurable : |
La σ-algèbre, ou algèbre de Borel ou encore tribu (appellation de Bourbaki) sera l'outil de base de la théorie de la mesure des parties d'un espace topologique. La mesure, au sens topologique, généralise la notion élémentaire de mesure d'un segment, ou d'une aire (au sens de Riemann ou de Jordan, par exemple) et est indissociable de la nouvelle théorie de l'intégration que Lebesgue mettra en place de 1901 à 1902.
Une σ-algèbre T, d'un ensemble E, est une famille de parties de E contenant E lui-même et stable par complémentation et réunion dénombrable, ce qui s'écrit :
E est élément de T;
si K est élément de T, alors il en est de même de CK aussi (complémentaire de K dans E);
si (Kn) est une suite (finie ou non) d'éléments de T, alors la réunion des Kn, de est élément de T.
Il est clair que toute intersection de tribus est une tribu et si F est un ensemble de parties d'un espace topologique X, parmi les tribus qui contiennent tous les éléments de F, il en existe une plus petite (au sens de l'inclusion) que toutes les autres, dite tribu engendrée par F : intersection de toutes ces tribus. C'est leur fermeture de Moore.
Espace mesurable :
On qualifie ainsi tout ensemble E muni d'une tribu T. On note souvent (E,T) un tel ensemble. Les parties mesurables de E sont les éléments de la tribu. Elles correspondent aux événements dans le cas d'un espace probabilisé.
∗∗∗
Soit f une application de E vers F
(E et F quelconques). Si A est une partie de F, on pose f-1(A) =
{x∈E / f(x)∈A},
image réciproque de a par f. Montrer que si T est une tribu de F, alors son
image réciproque par f
(ensemble des images réciproques de ses éléments) est
une tribu de E.
Application mesurable :
Si (E,T) et (F,τ) sont des espaces mesurables et f une application de E dans F, f est dite mesurable si l'image réciproque (cf. exercice ci-dessus) d'une partie mesurable de f est une partie mesurable de E :
∀ B∈τ , f-1(B) ∈T
Tribu borélienne, corps de Borel, application borélienne, espace borélien :
Dans un espace topologique X, on appelle tribu borélienne, ou tribu de Borel, la tribu engendrée par les ouverts de X. Ses éléments sont nommés boréliens (substantifs). Eu égard à la définition d'une σ-algèbre, elle est aussi engendrée par les parties fermées.
Lorsque X = R, on
peut montrer que la tribu borélienne est engendrée par les intervalles ouverts de la
forme ]α, +∞[,
α∈R
;
on peut même se contenter de choisir a dans un
ensemble partout dense de R : l'ensemble Q des rationnels, par
exemple. Pour désigner cette σ-algèbre
particulière, on parle parfois, mais ce n'est pas pertinent, de
corps de Borel.
Une application d'un espace topologique X vers un espace topologique Y est dite borélienne si l'image réciproque par f de tout borélien de Y est un borélien de X. Lorsque Y est métrisable et séparable, toute application de X dans Y est borélienne.
∗∗∗
Montrer que toute application continue f de R
dans R est borélienne.
➔ Un espace mesurable au sens de Borel est parfois qualifié d'espace borélien.
Mesure sur une tribu d'un espace topologique :
T désignant une tribu d'un espace topologique X, on appelle mesure sur (X,T) une application m σ-additive de T dans ]-∞, +∞]. La σ-additivité introduite par Borel exprime que pour toute réunion dénombrable ∪Kn d'éléments de T deux à deux disjoints (d'intersection vide) on a :
m(∪Kn ) = Σm(Kn)
Dans le cas d'espaces de Riesz de fonctions définies sur un espace topologique localement compact, on adjoint à la définition d'une mesure un axiome de continuité qu'utilisèrent systématiquement les mathématiciens « bourbakistes » :
Mesure de Radon : » Mesure de Haar : »
Mesure de Borel-Stieltjes :
F désignant une fonction numérique, croissante et continue à droite, on peut lui associer une
mesure µ, unique, vérifiantLorsque F admet une limite nulle en - ∞, F est appelée fonction de répartition de µ et si µ s'avère être une probabilité (cf ci-dessus), la limite en +∞ de F est 1. Lorsque F est l'application identique, on parle de mesure de Borel de la droite réelle :
µ(]a,b]) = b - a
Introduction à l'intégrale de Stieltjes : »
Tribu et espace probabilisé :
Si m est une mesure sur X, on m(Ø) = 0 et si, lorsque m est positive (c'est à dire m(K) ≥ 0 pour tout K de T), on a m(X) = 1, alors m s'identifie à une probabilité sur T et on parle de tribu d'événements. L'espace X, souvent appelé univers (et noté Ω) sur lequel est ainsi défini une probabilité est dit probabilisé et se note (X,T, m).
Kolmogorov et la définition axiomatique d'un espace probabilisé : »
∗∗∗
Soit X une
variable aléatoire discrète
(c'est à dire ne prenant qu'un nombre fini ou dénombrable de valeurs)
définie sur un espace
probabilisé Ω muni d'une tribu d'événements
T et à valeurs dans un ensemble E. Soit F une
partie de E.
Montrer que les ensembles {ω/ X(ω)∈F}
constituent une sous-tribu de T
(tribu engendrée par X).
Variables aléatoires indépendantes : »
|
Lien entre la mesure d'un ensemble et l'intégrale d'une fonction positive : |
 On note 1
On note 1
Si A est un intervalle de bornes a et b, la distance de a à b, a pour mesure b - a et coïncide avec l'intégrale au sens de Riemann de 1A car cette fonction vaut 1 pour tout x de [a,b] :
∫[a,b]
1A![]() dx
=
∫[a,b]
1.
dx
=
∫[a,b]
1.![]() dx = b
- a
dx = b
- a
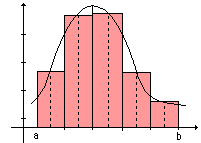
Dans le cas plus général d'une fonction f en escalier, l'intégrale de f sur [a,b] apparaît comme étant l'aire du domaine (mesure de sa surface) sous la "courbe" : d'où le principe d'intégration de Riemann en approchant une fonction par des fonctions en escalier.
➔ Pour en savoir plus :