ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Parabole & gravitation

On sait depuis les travaux de Kepler et de Newton que tout projectile lancé à une hauteur h du sol et soumis ensuite à la seule pesanteur tend à redescendre sur Terre suivant une loi horaire du second degré en t, t désignant le temps.

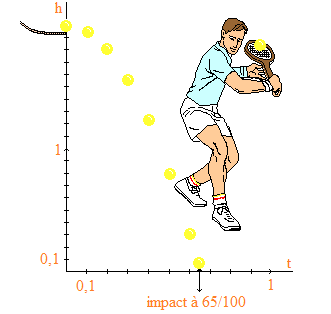
La trajectoire est donc parabolique (en forme de parabole) dépendant des conditions initiales (vitesse, angle par rapport à l'horizontale). On se propose de vérifier ce fait. Pour cela, on a photographié avec surimpression, une balle lancée sur un toboggan, tous les 1/10 e de secondes.

Sur le cliché reproduit ci-dessus, on a tracé des graduations (1 sec. = 1 unité en abscisse t, 1 m = 1 unité en ordonnée). Au temps t = 0, la balle abandonne le toboggan à la hauteur h_o = 2 m et est alors soumise à la pesanteur. L'impact au sol s'est produit après 65 centièmes de secondes.

Si la trajectoire est parabolique, son équation est de la forme :

où a, b et c sont à déterminer compte tenu de l'expérience. Ici b = 0 car l'axe des ordonnées est un axe de symétrie de la parabole. On calcule alors a et c en considérant les temps extrêmes.

Ce qui fournit c = 2 pour t = 0 et a × 0,65² + 2 = 0 lorsque t = 65/100. D'où a ≅ - 4,73 et c = 2. On trace la parabole d'équation d'équation t → - 4,73t² + 2. Il y a sensiblement coïncidence avec les observations :

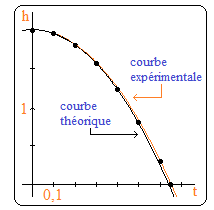
 ➔  D'après la loi gravitationnelle de Newton, le coefficient de t² dans h(t) = at² + bt + c est -½g où g ≅ 9,8 désigne l'intensité de l'accélération de la pesanteur au lieu considéré et c = h_o, la hauteur initiale. Il semble bien avoir concordance de cette la loi avec l'expérience, aux erreurs de repérage près inhérentes à ce type d'expérimentation, vu que -½g ≅ 4,9.