ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Tangentes communes à deux cercles, constructions & équations        TD niveau LYC/SUP        » Tangente au cercle : généralités & exercices

 ➔  La construction de la tangente commune à deux cercles de rayons distincts, éventuellement tangents extérieurement ou intérieurement, est étudié ici de façon élémentaire sans le recours à l'homothétie.

On considère donc, figure ci-dessous, deux cercles (c) et (c') ni sécants, ni tangents, ni inclus l'un dans l'autre, de centres et rayons C et r d'une part, C' et r' ≠ r d'autre part (les cas sécants, tangents et r = r' seront envisagés en fin d'étude).

Deux tels cercles sont homothétiques et il existe deux homothéties transformant (c) en (c'). Le point C doit avoir pour image C' : le centre d'une telle homothétie est donc situé sur (CC').

Soit M un point de C non situé sur (CC'). L'image de [CM] est [C'M'] avec M' sur (c') avec (CM) // (C'M') : il existe donc deux tels points M' et M'' diamétralement opposés : (MM') et (MM'') coupent (CC') respectivement en A et  en B.

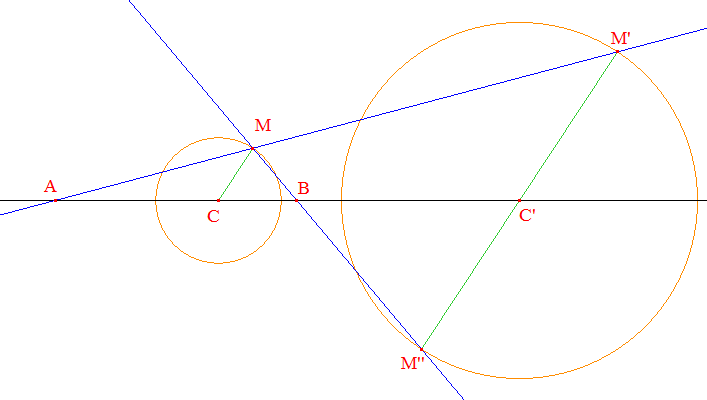
Le cercle (c) se transforme en (c') par les homothéties de centre A et de centre B. L'usage de la propriété de Thalès permet de calculer les rapports respectifs :

• AM'/ AM = AC'/ AC = C'M'/ CM = r'/r

• BC'/ BC = BM''/ BM = C'M''/ CM = -r'/r

Construction des tangentes communes extérieures :      

On sait que la tangente à un cercle (c) issue d'un point comme A ou B, est perpendiculaire au rayon aboutissant au point de contact. On peut vérifier cela en déplaçant M ci-dessus de sorte que (CM) soit perpendiculaire à (AM).

Par conséquent :

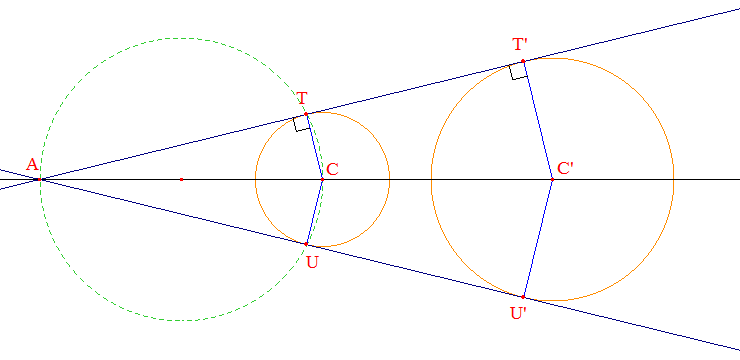
Pour obtenir le tracé des tangentes "extérieures" à (c) passant par A, on trace le cercle de diamètre [AC] qui coupe (c) aux deux points de contact T et U cherchés car les triangles ATC et AUC sont alors rectangles. L'homothétie conservant les angles (et les contacts), ces tangentes à (c) seront aussi tangentes à (c') aux points images T' et U'.
                 

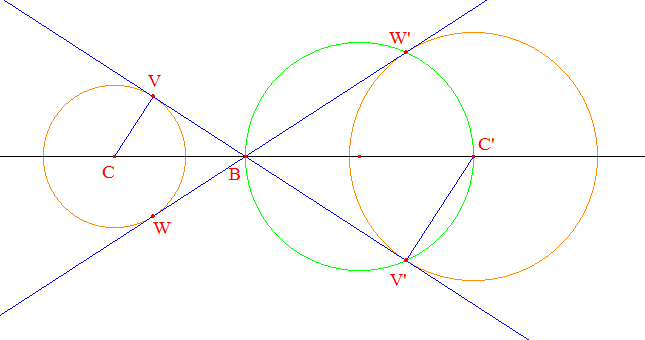
Une analyse semblable permet la construction des tangentes "intérieures" (VV') et (WW'). Ci-dessous, on a choisi de tracer le cercle de diamètre [BC'], ce qui fournit V' et W' puis les tangentes cherchées :

Synthèse :     

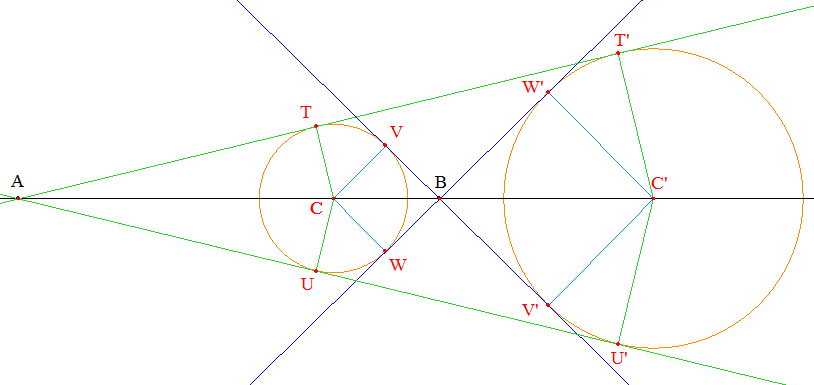
 ➔   Les tangentes extérieures d'une part et intérieures d'autre part sont symétriques par rapport à la droite des centres.

Équation des tangentes communes dans un repère orthonormé du plan :      

On se place dans un repère orthonormé d'origine O.

♦ Recherchons tout d'abord les équations des tangentes "extérieures". Comme vu ci-dessus, les cercles étant homothétiques dans l'homothétie de centre A de rapport r'/r, l'application du théorème de Thalès fournit la relation vectorielle r. AC' = r'. AC, d'où l'on tire facilement :

(r - r').OA = r.OC' - r'.OC

Il nous faut maintenant écrire que les tangentes cherchées passent par A. Une au  moins de ces tangentes possède une équation de la forme y - y_A = m(x - x_A) car nous avons supposé r' ≠ r . En effet, si les deux tangentes ne peuvent s'exprimer sous cette forme, alors elles sont toutes deux parallèles à (Oy) (équations de la forme x = k) et par suite r = r'. L'équation peut s'écrire mx - y +y_A - mx_A = 0.

Il nous suffit maintenant d'écrire que la distance de (c) -ou de (c')- à  cette droite est égale au rayon du cercle :

r² = (mx_C - y_C + y_A - mx_A)²/(m² + 1)

Cette égalité conduit en général à une équation du second degré en m fournissant les coefficients directeurs des tangentes cherchées. Si le coefficient de m² s'élimine (1er degré), alors une des tangentes est parallèle à l'axe des ordonnées.

☼  Exemple 1/4 :              

On a ici C(2;1), r = 1 et C'(5;3), r' = 2.

On calcule les coordonnées de A : OA = -1.(OC' - 2OC). Ce qui fournit A(-1;-1).

L'équation des tangentes "extérieures" est alors mx - y -1 + m = 0.

Puis r² = 1 = (3m - 2)²/(m² + 1). D'où l'équation 8m² - 12m + 3 = 0 fournissant m = (3 ± √3)/4.

Ci-contre, on a construit, au moyen du logiciel Cabri-Géomètre les tangentes à (c) et (c') par la méthode indiquée en début d'étude.

Le programme fournit alors une approximation rationnelle des coefficients directeurs : par exemple 84/71 = 1,1830... ≅ (3 + √3)/4 (à 10^-4 près).

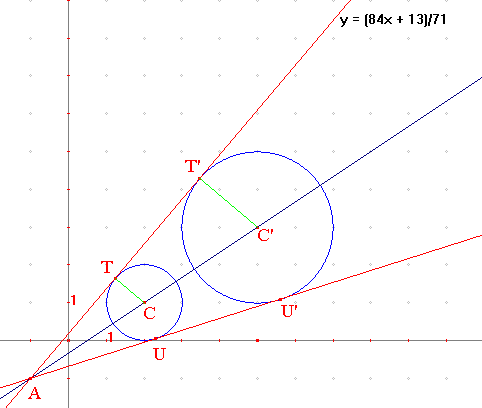
☼  Exemple 2/4 :           

On a ici C(3;1), r = 1 et C'(4;5), r' = 2.

On calcule les coordonnées de A : OA = -1.(OC' - 2OC). On obtient A(2;-3).

L'équation des tangentes "extérieures" est alors mx - y - 2m - 3 = 0.

Puis r² = 1 = (m - 4)²/(m² + 1). D'où l'équation 8m = 15 : les m² s'éliminent. Une des tangentes est parallèle à l'axe des ordonnées. Comme elle passe par A, son équation est x = 2.

Ci-contre, on a construit, au moyen du logiciel Cabri-Géomètre les tangentes à (c) et (c') par la méthode indiquée en début d'étude.

Le programme fournit la valeur exacte  m = 15/8 du coefficient directeur de la seconde tangente dont l'équation est y + 3 = (x - 2) × 15/8, soit

y = 15x/8 - 3 - 15/4 ou encore y = 15x/8 - 27/4

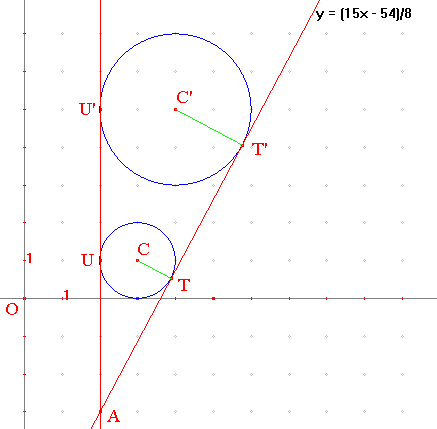
♦ Le cas des tangentes "intérieures se traite de la même façon : la seule différence est le rapport négatif d'homothétie. L'application du théorème de Thalès fournit ici la relation vectorielle r. BC' = -r'. BC, d'où l'on tire facilement :

(r + r').OB = r.OC' + r'.OC

La suite des calculs est identique au cas "extérieur".

☼  Exemple 3/4 :            

On reprend l'exemple 1. On constate graphiquement qu'une tangente commune "intérieure" est la droite d'équation x = 3. Notre équation en m devrait donc être du 1er degré.

Vérifions cela : on a 3OB = OC' + 2OC. D'où B(3;5/3). L'équation de la tangente cherchée passant par B, son équation est de la forme mx - y + y_B - mx_B, soit mx - y + 5/3 - 3m = 0.

On obtient l'équation d'inconnue m : r² = (mx_C - y_C + y_B - mx_B)²/(m² + 1), soit m² + 1 = (-m + 2/3)². Les m2 s'éliminent et m = -5/12 est l'unique solution. On en déduit l'équation de la tangente cherchée :

y = -5x/12 + 35/12 = (-5x + 35)/12

• En cas de cercles sécants, il ne reste que deux tangentes "extérieures" dont l'approche est la même que dans le cas non sécants.

• Si les cercles sont tangents extérieurement en un point A, nous avons une tangente "intérieure" passant par A perpendiculaire en A à la droite des centres. L'étude des tangentes extérieures est identique au cas général.

• Si les cercles sont tangents intérieurement : il existe une unique tangente en A perpendiculaire à (CC').

Lorsque les cercles ont même rayon, le milieu B de [C,C'] est un centre de symétrie de la figure : on passe de (c) à (c') par symétrie centrale de centre B. On peut aussi parler d'homothétie de rapport -1.

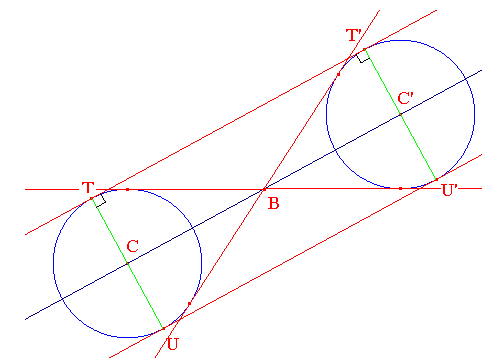
• Les tangentes intérieures et leurs équations s'obtiennent donc comme dans le cas général.

• Concernant les tangentes "extérieures", tout se passe comme si le point A était rejeté à l'infini. Si l'on considère la tangente (TT'), on a (CT) ⊥ (TT'), (C'T') ⊥ (TT') et CT = C'T'. Par suite CTT'C' est un rectangle. les points de tangence T, T', U et U' s'obtiennent alors en traçant les perpendiculaires à (CC') en C et C'.
  
  Leurs équations s'obtiendront facilement : si C et C' ont même abscisse, le cas est évident. Sinon, (CC') possède une équation y = mx + p et celles des tangentes "extérieures" seront de la forme y = mx + q. On écrira là encore que la distance de (c) -ou de (c')- aux tangentes est égale au rayon du cercle :

  r² = (mx_C - y_C + q)²/(m² + 1)

ce qui fournira les deux valeurs de p.

☼  Exemple 4/4 :         

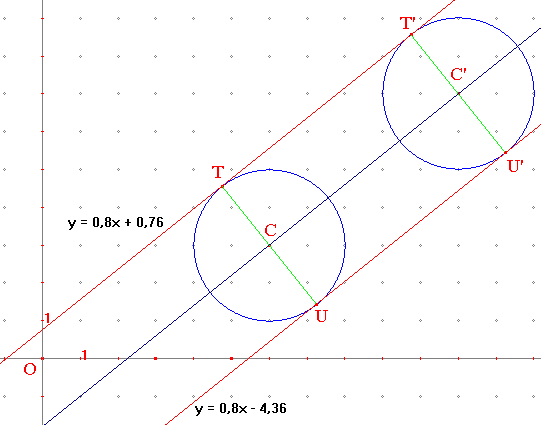
On a ici r = r' = 2, C(6;3), C'(11;7). Le coefficient directeur de la droite des centres est donc (7 - 3)/(11 - 6) = 4/5 = 0,8. L'équation des tangentes cherchées sont alors de la forme y = 0,8x + q.

On obtient l'équation d'inconnue m : r² = (0,8x_C - y_C + q)²/(0,8² + 1), soit 6,56 = (1,8 + q)². On en déduit : q = -1,8 ± 4√0,41 et, en valeurs approchées avec √0,41 ≅ 0,64, les équations des tangentes confirmées par le logiciel Cabri-Géomètre :

y = 0,8x + 0,76    et    y =  0,8x - 4,36