
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

On considère l'hélice circulaire (H) d'équation :
Elle s'enroule donc sur le cylindre de révolution d'axe (Oz), de base le disque de centre O de rayon r. Soit (C) le cône de révolution de sommet O, de hauteur h inscrit dans le cylindre.
Pour tout point P de (H), on note K sa projection orthogonale sur l'axe (Oz) et on appelle M le point d'intersection de [PK] avec le cône (C). Quel est l'ensemble des points M ?
Une simple application du théorème de Thalès conduit à la solution :
![]()
» Ci-dessus, à droite, le projet (en bois) d'une tour hélicoïdale imaginée par le peintre et sculpteur russe Vladimir Tatline (1885-1953) à la gloire de la IIIè Internationale. Sa hauteur aurait dépassée celle de la tour Eiffel ! image empruntée sur le site de l'université d'Auburn (Alabama, USA), page de George Mitrevski.
|
L'hélice circulaire et la spirale conique en choisissant respectivement r = 1, h = 40 et r/h = 1 : |
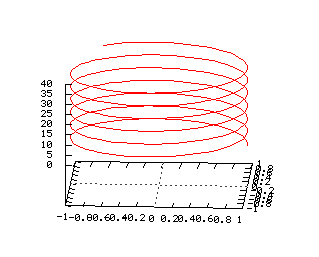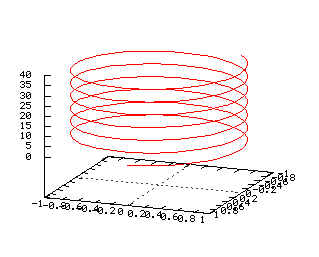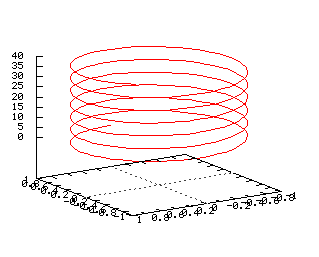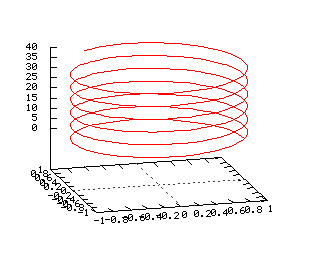
= Animations générées par wims =
» on remarquera que la projection sur le plan des XY de cette spirale n'est autre qu'une spirale d'Archimède, dont l'équation polaire r = a x t fournit en représentation paramétrique :
Le paramètre a représente ici r/h.


Minaret de la mosquée «
Al-Malwiyah » (Samarra, Irak)
mot à mot : « La torsadée », 9è siècle