ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 
Théorème de Fourier,
également dit de Budan-Fourier» Budan de Boislaurent |
Théorème :
Soit P(x) = 0 une équation polynomiale de degré n à coefficients réels, a et b, a < b, deux réels tels que P(a) et P(b) soient non nuls.
P(k) désignant la dérivée k-ème de P, on note V(x) le nombre de changements de signe dans la séquence [P(x), P'(x), P''(x), ..., P(n)(x)]. Dans ces conditions :
V(a) ≥ V(b)
Si V(a) = V(b) : il n'y a aucune racine dans l'intervalle [a,b]
Si V(b) - V(a) = 1 : l'équation possède une racine unique dans ]a,b[
Si V(b) - V(a) = 2 : l'équation possède deux racines réelles ou complexes dans ]a,b[
Si V(b) - V(a) = 3 : l'équation possède une racine réelle ou trois racines dont deux complexes dans ]a,b[
Plus généralement, le nombre de racines réelles dans l'intervalle ]a,b[ est au plus égal à δ = V(b) - V(a).
➔ Une racine multiple, par exemple double, compte pour deux. Fourier précise que si le nombre effectif N de racines s'avère strictement inférieur à V(a) - V(b), alors la différence δ - N apparaît paire : cela correspond à l'existence de racines complexes conjuguées apparaissant par paires puisque les coefficients de l'équation sont des nombres réels. On peut ainsi écrire δ ≤ n et la congruence δ ≡ V(b) - V(a) [mod. 2].
Exemple :
Considérons P(x) = 360x4 - 342x3 + 119x2 - 18x + 1. On s'intéresse aux intervalles [0;1], [0;0,3] et [0,3;1]. On a :
- P'(x) = 1440x3 - 1026x2 + 238x - 18.
- P''(x) = 4320x2 - 2052x + 238
- P(3)(x) = 8640x - 2052
- P(4)(x) = 8640
| en 0 | en 1 | en 0,3 | |
| P | + | + | - |
| P' | - | + | - |
| P" | + | + | + |
| P(3) | - | + | + |
| P(4) | + | + | + |
| V | V(0) = 4 | V(1) = 0 | V(0,3) = 1 |
On déduit du tableau qu'il y a :
Au plus 4 racines réelles entre 0 et 1 et plus précisément 0, 2 ou 4;
En effet, P a été fabriqué comme étant :
P(x) = 360(x - 1/6)(x - 1/5)(x - 1/4)(x - 1/3)
Et une approche graphique permet d'éliminer ou confirmer la présence de racines complexes :
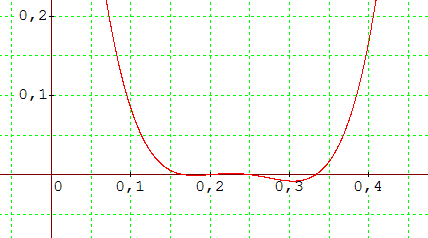
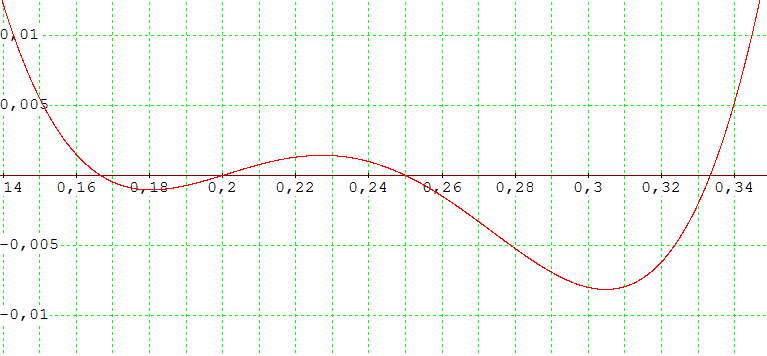
Il y a manifestement 4 racines réelles : on peut donc confirmer les résultats du tableau.
|
De la paternité de ce théorème : |
On
parle parfois de théorème de Budan-Fourier. Il semble que cela soit injuste et
faux. Le mémoire de Budan (1806) ne contient nullement le théorème en question
mais un critère plutôt vague utilisant des transformations de l'équation au
moyen des variables x - 1, x - 2, ... ou x - p.
On peut le constater sur Gallica : voir la page consacrée à
Budan de Boislaurent.
Selon Darboux, à la page 310 de ce document numérisé : Oeuvres complètes de Fourier, Fourier enseignait déjà son théorème en 1796,1797 et 1803 à l'École polytechnique, mais sans l'avoir officiellement publié (très imprudent...). Darboux estime "absolument insignifiant" l'apport de Budan sur le sujet...
En 1807, Poisson écrit à Fourier qu'un "docteur en médecine vient de publier un Ouvrage sur la résolution numérique des équations et conseille à Fourier de publier officiellement son théorème et Sturm rend hommage à Fourier en reconnaissant s'être appuyé sur son travail pour élaborer son théorème sur le même sujet.
En 1811, Budan présente à l'Académie des sciences un mémoire plus complet sur le sujet toujours basée sur les transformées en x - p. Fourier ne publie le sien qu'en 1820 : Sur l'usage du théorème de Descartes dans la recherche des limites des racines. Il est suivi d'une nouvelle édition de Budan en 1822, peu convaincante : on pourra consulter le mémoire sur Gallica2 en page 291. La démonstration du théorème apparaît à partir de la page 295. Voir la conclusion de Budan, page 91.
Le théorème de Sturm (1829) : »