
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges


en rose r = sin(2t/3) , en bleu r = cos(2t/3)
| Étude de deux courbes : r = sin(2t/3) et r = cos(2t/3) |
3π étant la période commune de cos(2t/3) et sin(2t/3), l'étude théorique de ces courbes se fera sur le plus petit multiple commun à 2π et 3π, soit sur [0,6π].
Cependant, concernant par exemple r = sin(2t/3), on peut remarquer que :
r(3π - t) = r(6π - t) = -r(t)
C'est dire que les droites polaires t = (3π - π)/2 ≡ π et t = (6π - π)/2 ≡ π/2, donc Ox et Oy, sont des axes de symétrie de la rosace : on restreint alors l'étude de la courbe à [0,3π/2] (en rouge), on symétrise par rapport à (Ox) (en vert), puis on symétrise l'ensemble par rapport à (Oy) (en bleu).
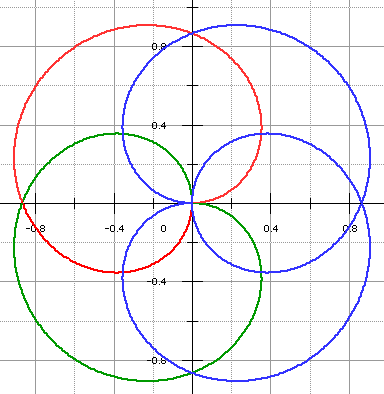
➔ Notons d'autre part : r(t) = r(3π/2 - t) = r(9π/2 - t) : les bissectrices des axes (correspondant à t = 3π/4 ≡ -π/4 et t = 9π/4 ≡ π/4) sont aussi des axes de symétrie.
| Un autre joli cas de superposition : r = 2cos(3t/2) et r = 2,5sin(6t) |

en rose r = 2,5sin(6t) , en bleu r = 2cos(3t/2)