ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Notion de valeur moyenne, moyenne pondérée, vitesse moyenne    TD niveau 6ème/5ème

La valeur moyenne m (on dit aussi moyenne tout court) d’une série de n nombres a₁, a₂, ... , a_n est égale à la somme de ces nombres divisée par n :

•  La moyenne des deux nombres 5 et 7 est 6 : 

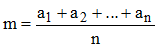
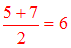
• La moyenne de 7, 10 et 13 est (complète...) :

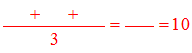
Une moyenne ne tombe pas toujours juste. Dans ce cas, en général, on arrondit le résultat à 0,1 près (au dixième) ou 0,01 près (au centième), etc. suivant les cas. Par exemple, la moyenne des notes d’un élève est souvent arrondie au dixième ou à 0,5 près. Il faut savoir qu’un arrondi se fait toujours au plus proche de la précision souhaitée :

• Romain  est un bon élève, en maths en tout cas : il a eu 18, 14, 17, 18, 15 et 17 en contrôle. Quelle est sa moyenne arrondie à 0,1 près ? Quelle est sa moyenne arrondie à 0,5 près ? Rép. : La moyenne de Romain est (18 + 14 + 17 + 18 + 15 + 17)/6 = 97/6. La calculatrice fournit 16,16666... Arrondie à 0,1 près, la moyenne de Romain est 16,2 et à 0,5 près sa moyenne est 16.

Moyenne pondérée, coefficients :  

Dans une série de nombres, certains peuvent apparaître plus que d’autres : on dit qu'ils n'ont pas le même "poids". On parle aussi de coefficient. Un coefficient 2 indique que le nombre doit être compté deux fois : il compte double. Un coefficient 3 indique que le nombre doit être compté trois fois :  il compte triple, etc. Pour exprimer que des nombres n'ont pas le même coefficient, on parle de moyenne pondérée.

La moyenne pondérée de la série de nombres 2, 3, 3, 5, 5, 5, 5 :

Les nombres qui se répètent sont comptés pour autant de fois. Dans cet exemple, le 2 a pour coefficient 1, le 3 a pour coefficient 2, le 5 a pour coefficient 4.

•  Paul a eu 11/20, 13/20 aux contrôles de mathématiques (coefficient 1), 8/10 à un test (soit 16/20, coefficient 1/2) et 12/20 à un devoir de deux heures (coefficient 2). Sa moyenne sera (11 + 13 + ½16 + 2 × 12)/(1 + 1 +½ + 2), soit 12,44 que l'on peut arrondir à 12,5.

• Pierre a eu 18 et 16 en interrogation écrite et 12 seulement à un contrôle bilan. Le professeur a dit que le contrôle bilan entrait dans la moyenne avec un coefficient 2. Quelle est la moyenne de Pierre ? Quelle aurait été sa moyenne (à 0,5 près) si le contrôle bilan avait compté comme les autres notes ?
  Rép. : avec le contrôle bilan compté coefficient 2, la moyenne de Pierre est (18 + 16 + 24)/4 = 14,5. Si le contrôle bilan perd son coefficient 2, alors sa moyenne est (18 + 16 + 12)/3 = 15,3333, soit 15,5 à 0,5 près.

∗∗∗
1.  Étienne est un enfant très doué : Jusqu'ici, il a eu 4,5/5 à chaque interrogation écrite de maths. Mais au dernier test, il s'est complètement planté : il a eu 2/5.
En travaillant dur, il espère obtenir prochainement que des 5/5. Combien en faudra-t-il pour retrouver sa moyenne de 4,5 ?  ☼
2. Papy a fait une balade en vélo d'appartement : il a roulé 10 minutes à 25 km/h et 20 minutes à 16 km/h. Quelle est sa vitesse moyenne ? ☼

La moyenne des notes obtenues dans les diverses matières résume mal le niveau d’un élève sans pour autant donner d’indications précises. 9 et 11 ont pour moyenne 10. Tout comme 18 et 2. Plus généralement, indiquer la moyenne de la classe dans chaque matière en faisant la moyenne des moyennes des élèves n'a guère de sens car la présence dans la classe de très "bons" ou très "mauvais" élèves fausse l'appréciation. Raison pour laquelle les mathématiciens statisticiens ont inventé des critères complémentaires comme l'écart-type, mesurant la dispersion autour de la moyenne.

 ➔  D'une façon générale, à la manière des problèmes barycentriques, la moyenne pondérée des nombres a₁, a₂, a₃, ..., a_n de coefficients (poids) respectifs p₁, p₂, p₃, ..., p_n est le nombre :

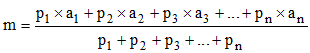
Lorsque les poids sont égaux, on retrouve la moyenne arithmétique, équivalente à des p_i tous égaux à 1.

La notion de vitesse moyenne :    

La vitesse d'un objet, d'un véhicule, d'un animal ou d'une personne n'est pas toujours constante :

• si vous roulez ½h à 100 km/h puis ½h à 80 km/h, tout se passe comme si vous aviez roulé 1 heure à 90 km/h.

• si vous roulez 2h à 130 km/h et 1h à 70 km/h, vous avez roulé 3 heures et parcouru 330 km : c'est comme si vous aviez roulé 3 heures à 110 km/h : c'est votre vitesse moyenne sur le parcours. En appliquant la formule des moyennes pondérées, cela s'écrit :

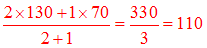
• Si le bus de Pierre l’amène au collège en 20 minutes pour une distance de 18 km, la question  « Quelle a été sa vitesse en km/h (kilomètre par heure) ? »  n’a pas de sens car on ne roule pas toujours à la même vitesse ! C’est pourquoi on parlera ici de vitesse moyenne :  la question sera alors  « Quelle a été sa vitesse moyenne en km/h ? ». Sachant que 1h = 60 min = 3 x 20 min, 18 km en 20 minutes font 3 x 18 km en 3 x 20 minutes, c’est à dire 54 km/h en moyenne.

∗∗∗
La  sonde américaine Cassini a été envoyée vers Saturne en octobre 1997. Elle est arrivée près de la planète début décembre 2004.
En arrondissant, on peut dire qu’elle a parcouru 3 milliards de km en 7 ans. Pourrais-tu calculer sa vitesse moyenne en km/h ? (utiliser 1 année = 365 jours et  arrondir à la centaine). Convertis ensuite cet arrondi en km/s (kilomètres par seconde) en arrondissant à l'unité. Tu as droit à la calculatrice ! ☼