
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» Utiliser le programme JavaScript on line |
On se propose d'étudier un algorithme très efficace pour la recherche du minimum et du maximum d'une fonction numérique sur un intervalle fermé borné [a,b]. Nous procédons ici par trisection : f désigne une fonction partout définie sur [a,b]. On note h = b - a. Calculons yp = f(a + h/3) et ym = f(b - h/3).
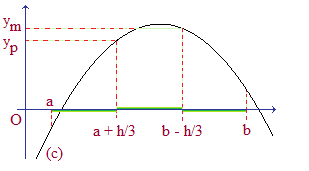
Si yp ≤ ym, on peut exclure le premier tiers de l'intervalle [a,b] et on recommence en remplaçant a par a + h/3. Sinon, on exclut le dernier tiers et on recommence en remplaçant b par b - h/3.
pour la seconde recherche, l'amplitude de l'intervalle est 2/3 x h.
pour la troisième recherche, il sera de 2/3 x 2/3.h = (2/3)2 x h.
pour la n-ème, l'amplitude sera (2/3)n - 1 x h.
C'est le terme général d'une suite géométrique de raison positive, inférieure à 1 : l'amplitude tend vers 0. C'est dire que le procédé converge vers un intervalle réduit à un point xo pour lequel f est maximale. Dans la pratique on s'arrête si h est inférieur à une précision fixée par l'utilisateur. Nous choisissons ici h = 10-6.
➔ Mais comment trouver le minimum de f sur [a,b] ? c'est tout simplement le maximum de -f !
| Programmation de la méthode en JavaScript |
➔ Pour tester ce programme vous devez entrer votre fonction en utilisant une syntaxe comprise par le langage JavaScript. L'instruction with (Math), placée en début de procédure, évite à l'utilisateur de préciser Math devant chaque fonction mathématique utilisée. Les opérations et fonctions usuelles sont les suivantes :
multiplication : * , division : /
racine carrée : sqrt(x)
puissance : pow(x,n). Pour x2 ou x3, utiliser plutôt x*x et x*x*x
fonctions usuelles : sin(), cos(), tan(), atan(), abs();
log népérien : log() , exponentielle de base e : exp() , ...
les appellations pi (pour π) et e sont comprises par le programme.
Par défaut, la fonction fournie au programme est y = ln2(x) + x admettant un minimum absolu
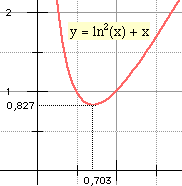
On a f '(x) = 2 ln(x)/x + 1. Une étude élémentaire permet d'affirmer que f admet un minimum lorsque 2ln (x) + x = 0, soit lorsque ln(x) = -x/2. Ce minimum est atteint pour un x compris entre 0 et 1 (car il faut ln x < 0). On lance le programme avec a = 0,1 et b = 1 en fournissant la fonction :
Le résultat est quasi instantané : on obtient le minimum 0,82718 en x ≅ 0,70356.
|
<SCRIPT LANGUAGE=JavaScript> var fonc,pi,e pi=3.141592653589793; e=2.7182818284590452; function go() { with (Math) { fonc="-log(x)*log(x)-x" a=0.1 ; b=1; fonc=prompt("Entrez votre fonction :",fonc) a=eval(prompt("Entrez a :",a)) b=eval(prompt("Entrez b :",b)) h=b-a; while(h>1e-6) { yp=f(a+h/3);ym=f(b-h/3) if (yp<=ym) {a=a+h/3} else {b=b-h/3} h=b-a; } x=(a+b)/2; y=f(x); alert("Max f = "+arr(y)+" en x = "+arr(x)) } } function f(x) {with(Math) {y=eval(fonc) ; return y}} function arr(x) </SCRIPT> |