ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Lemniscate de Bernoulli      » lemniscate en tant qu'inverse de l'hyperbole , lemniscate en tant que podaire de l'hyperbole , courbes cycliques

Jakob Bernoulli fut amené à définir, comme le fit indépendamment Newton, la notion de coordonnées polaires avec l'introduction de sa lemniscate (du grec lemniskos = ruban) :

Soit F'(-a,o) et F(a,o), la lemniscate est l'ensemble des points M du plan tels que MF × MF' = a². Ci-dessous a = 1 :

F'(-1,o) et F(1,o), ensemble des points M du plan tels que MF ×MF' = 1 et ses tangentes y = ± x en O.

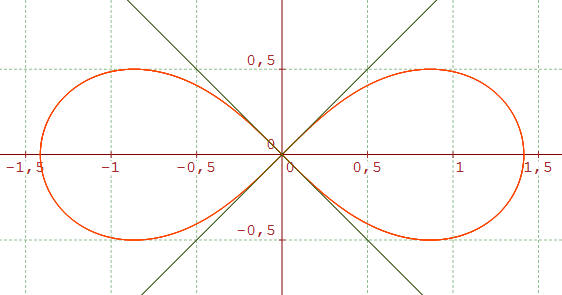
En coordonnées polaires, la lemniscate a pour équation : r² = 2a²cos2t. La lemniscate ci-dessus (a = 1) est obtenue entièrement tout aussi bien par r = (2cos2t)^1/2 que par r = - (2cos2t)^1/2, t variant de 0 à 2π ou de - π à +π.

On peut réduire l'intervalle d'étude à [0,π] car cos(2t) = cos [2(t + π)] : symétrie par rapport à O. Mais cos(2t) = cos [2(π - t)] : symétrie par rapport à Oy : on peut alors limiter l'étude à [O,π/2] et même à [0,π/4] car r² est positif et compléter la courbe par une symétrie par rapport à O puis par rapport à Oy.

Lemniscatographe sur YouTube :  »

Équation implicite :   

Cette jolie courbe est un cas particulier d'ovale de Cassini. En développant MF² × MF'² = a⁴, on obtient facilement son équation cartésienne. C'est une quartique bicirculaire :

(x² + y²)² - 2a²(x² - y²) = 0     » tangentes en O(0,0)

Bernoulli exprima l'équation sous la forme :

En posant x = r.cos t et y = r.sin t, on a immédiatement l'équation polaire : r² = 2a²cos 2t. L'aire d'une boucle est a²/2.

On trouve parfois la lemniscate sous la forme r² = 2a²sin 2t : image de la précédente par une rotation d'angle π/4, représentée ci-dessous. On remarquera que cos 2t = sin 2(π/4 - t).

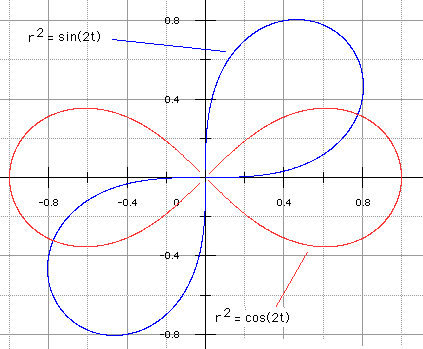
On a choisi a = 1/√2, soit 2a² = 1.

Dans le cas général, on pourra vérifier que le cercle de centre O, de rayon a coupe la lemniscate en ses 4 points d'élongation maximale en y. Les tangentes en 0, point double, sont perpendiculaires.

Équation paramétrique :   

Rechercher une équation paramétrique de la forme x = f(t), y = g(t) est un peu plus délicate... On a :

et, quitte à compléter par symétries, on peut supposer t∈[0,π/4] , afin d'avoir cos 2t non négatif. On pose alors u = tan t. Dans ces conditions, u varie de 0 à 1 et on a les formules élémentaires de l'arc moitié (t et ici la moitié du double...):

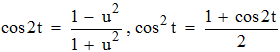
En remplaçant dans x² exprimé précédemment, on trouve facilement :

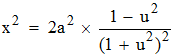
Afin d'exprimer x² sous la forme d'un carré, posons maintenant u = sin θ, loisible car u varie de 0 à 1; on a θ = Arcsin(tan t), qui varie alors de 0 à π/2, et

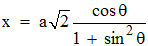
En éliminant la possibilité opposée non utile, car si θ varie de π/2 à π la détermination ci-dessus fournit la valeur opposée (négative de x) que nous voulions (symétrie par rapport à O). Il s'agira alors de choisir la bonne détermination de y. Sachant que :

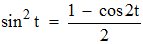
un calcul analogue fournit :

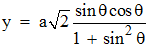
En conclusion :   

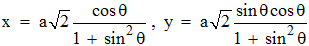,    θ ∈[0,2π]

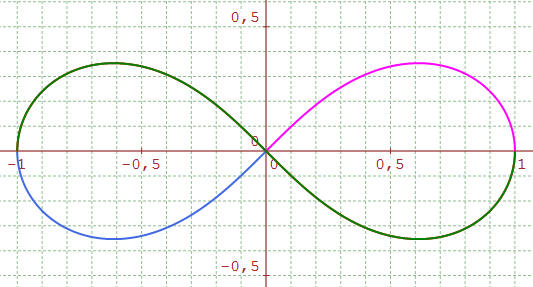
On a choisi a = 1/√2. magenta : θ ∈[0,π/2], bleu : θ ∈[π/2,π] (sym./O) , vert : θ ∈[π,2π] (sym/Ox)

Sous la forme r² = 2a²sin 2t : la rotation de centre O, d'angle π/4, d'expression analytique x' = (x - y)/√2 , x' = (x + y)/√2 conduit à :

---

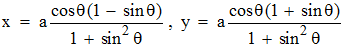
 ➔  Certains diront que la lemniscate est unicursale car son genre est nul et devrait donc admettre une paramétrisation rationnelle. Exact. On établira facilement cette représentation en posant dans l'équation précédente t = tan(θ/2) et en utilisant les formules élémentaires de l'arc moitié (on a choisi a = 1/√2) :

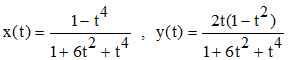
On pourra également consulter la page consacrée au mathématicien allemand Alfred Clebsch afin de retrouver directement cette équation en utilisant des résultats adaptés aux courbes algébriques unicursales.

Lemniscate de Bernoulli en tant qu'inverse de l'hyperbole :

L'inversion de pôle O de rapport a√2 transforme la lemniscate en l'hyperbole équilatère :

x² - y² = 2a²

dont les foyers sont les images des foyers de la lemniscate.

Montrons ce résultat dans le cas 2a² = 1 (soit a = 1/√2) afin de simplifier les calculs. On a, avec les notations ci-dessous :

• lemniscate : r² = cos 2t, soit OM² = cos 2t

• hyperbole équilatère : x² - y² = 1. nous pouvons paramétrer la courbe en posant x = 1/cos u et y = tan u. Ce n'est pas le même paramètre ! Or, pour cette hyperbole : tan t = y/x = sin t. On en déduit : OM'² = 1/cos²u + tan²u = (1 + tan²t)/(1 - tan²t) et on vérifie facilement que ceci n'est autre que l'inverse de cos 2t.

Par suite OM² × OM'² = 1 : on passe de la lemniscate à l'hyperbole par l'inversion de pôle O, de rapport 1. Le foyer de la lemniscate d'abscisse positive, est ici en (√2/2;0) et celui de l'hyperbole équilatère est en (√2;0). Ils s'échangent donc bien dans l'inversion.

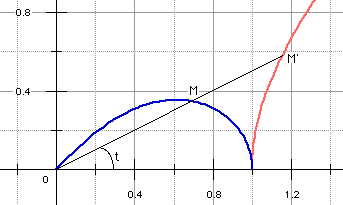
 ➔  Enfin, on peut aussi montrer que la podaire par rapport à O de l'hyperbole équilatère est la lemniscate :