ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Kampyle d'Eudoxe (du grec kampulos = courbé)        » Voir l'animation

Eudoxe de Cnide s'intéressa à la duplication du cube dans le cadre de sa théorie des proportions. Rappelons ce célèbre problème de l'Antiquité grecque :

La ville de Délos possédait un autel cubique à la gloire d'Apollon. Afin de débarrasser la ville d'une épidémie de peste, l'oracle avait exigé la construction d'un autel  exactement deux fois plus grand en volume.

Le problème de la duplication du cube revient à la construction de la racine cubique de 2 car si :

V = c³  alors (c × ³√2)³ = 2V.

Étant donnés deux nombres a et b, il est aisé de construire géométriquement, au sens euclidien de la règle et du compas, la moyenne proportionnelle de ces deux nombres, c'est à dire une mesure m tel que :

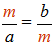
 ➔    Euclide n'entrera en scène qu'un siècle plus tard mais le concept platonicien de la pureté géométrique (le non usage des nombres et des mesures) était déjà installé. Eudoxe fut un contemporain de Platon qui lui enseigna la géométrie.

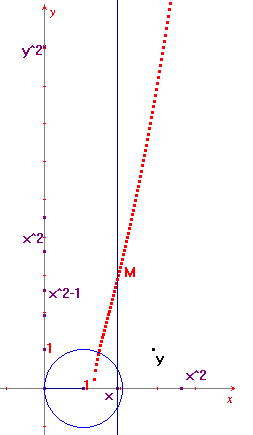
Supposons alors construits au voisinage de x = 1, un grand nombre de points y, placés en ordonnée, tels que :

Ces points appartiennent à la courbe d'équation y² = x⁴ - x² (courbe algébrique de degré 4) : c'est le kampyle d'Eudoxe, obtenu à droite par Cabri-Géomètre (» animation).

Intersectons celui-ci avec le cercle de centre I(1;0) de rayon 1; on obtient la racine cubique de 2 (sensiblement 1,26) :

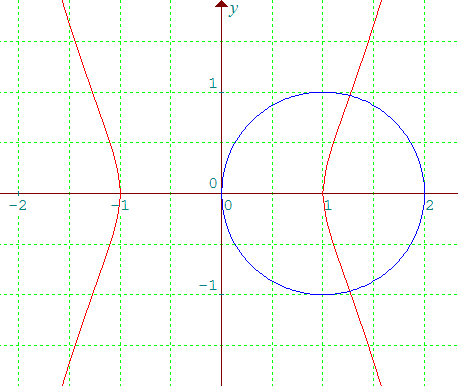
La courbecomplète,  tracée par Graphmathica.

Comme tous les procédés imaginés brillamment par les Grecs de l'antiquité pour contourner l'impératif platonicien de la règle et du compas, la méthode relève de l'approximation successive; on sait depuis Wantzel que la solution voulue par Platon n'existe pas !

La courbe est générée au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa version CabriJava pour Internet. On a utilisé la propriété de Thalès et les moyennes proportionnelles pour placer x² et y², puis x² - 1 (par cercle de centre x² de rayon 1) et y en tant que racine carrée de y² dans un repère orthonormé :

Si votre navigateur accepte les applets Java (» extension CheerpJ) :
Déplacer x; pour effacer le lieu double-cliquer dans la figure