
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
» les valeurs en gras italique désignent des vecteurs. On suppose ici connue la notion de courbe gauche ainsi que le vocabulaire et les propriétés de base y afférant (tangente, normale, plan osculateur, courbure, ....).
L'espace euclidien usuel de dimension 3 étant rapporté à un repère orthonormé (O, e1, e2, e3). On considère une courbe de l'espace 3D, courbe gauche parcourue par un point M(t), fonction du paramètre t variant dans un intervalle J :
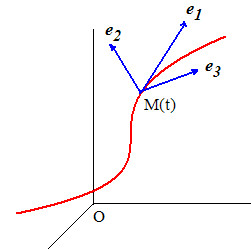
On suppose M(t) régulier pour tout t de J : les coordonnées de M sont continûment dérivables sur J et et ne s'annulent pas simultanément. L'idée de Frenet fut d'étudier la courbe dans un repère orthonormé mobile d'origine M dont les vecteurs, notés provisoirement e1, e2 et e3, sont des fonctions continûment dérivables de t avec la condition que e1 dirige la tangente en M à la courbe. Dans ces conditions, on doit pouvoir écrire :
dei/dt = ai,1.e1 + ai,2.e2 + ai,3.e3 (i = 1, 2, 3)
dM/dt =
Préliminaire :
Soit u(x,y,z) et v(X,Y,Z) deux vecteurs dont les coordonnées sont des fonctions dérivables de t et dont le produit scalaire <u,v> est constant. On note u'(x',y',z') et v'(X',Y',Z') les dérivées par rapport à t. Vérifier que <u',v> + <u,v'> = 0.
Déterminons maintenant les dei/dt en tenant compte des contraintes orthonormales : tout d'abord, le produit scalaire < ei , ej > est nul si i distinct de j (et vaut 1 si i = j). On en déduit par dérivation que < ei , dej/dt > + < dei/dt , ej > = 0 et, en particulier, < ei , dei/dt > = 0 : ei est orthogonal à son vecteur dérivé.
Or < dei/dt , ej > = < ai,1.e1 + ai,2.e2 + ai,3.e3 , ej > = ai,j. On en déduit ai,j = - aj,i : la matrice des coordonnées est donc antisymétrique ce qui entraîne ai,i = 0. pour i = 1, 2, 3.
Posons maintenant ds = α.dt. Dans ces conditions dM/ds = e1
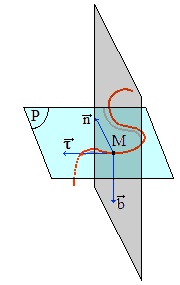
Dans le plan orthogonal à e1 = τ, choisissons notre second vecteur e2 en remarquant que dτ/dt fait partie de ce plan : notre second vecteur de base e2 sera choisi unitaire et de même sens que dτ/dt. Il s'agit de la normale principale à la courbe, nous le notons désormais n. On a alors dτ/dt = de1/dt = a1,2.n : la coordonnée a1,3 est nulle, donc aussi a3,1.
Utilisons l'abscisse curviligne :
dτ/dt = dτ/ds × ds/dt = a1,2.n, ce qui conduit, en posant K = a1,2.dt/ds, à dτ/ds = K.n
Soit b =
τ ^ n,
la binormale, produit vectoriel de
τ
par n. Le trièdre (τ, n, b)
est ainsi orthonormé direct (par rapport au repère initial d'origine O). Posons aussi T = a2,3.dt/ds;
on a alors :
de2/ds = dn/ds
= a2,1.e1 + a2,3.e3
= -
a1,2.e1 + a2,3.e3
=
-K.τ + T.b
Enfin, vu a3,1 = a3,3 = 0, il reste : de3/dt = a3,2.e2 = - a2,3.e2, d'où db/ds = - T.n
Soit, sous forme matricielle :
Interprétation du nombre K défini par dτ/ds = K.n
: dτ/ds =
d2OM/ds2 = K.n.
Par conséquent : K2 = ||
d2M/ds2 || = (d2x/ds2)2
+ (d2y/ds2)2 +(d2z/ds2)2 Montrons que K est la courbure
en M(s) : on sait qu'elle est la limite du rapport Δâ/Δs
lorsque tend Δs
vers 0. Or, si on note
cos Δâ = α(α + Δα) + β(β + Δβ) + γ(γ + Δγ) » cosinus directeurs, 4°
et l'identité de Lagrange permet d'écrire :
sin2Δâ = [α(β + Δβ) - β(α + Δα)]2 + [β(γ + Δγ) - γ(β + Δβ)]2 + [γ(α + Δα) - α(γ + Δγ)]2
= (αΔβ - βΔa)2 + (βΔγ - γΔβ)2 + (γΔα - αΔγ)2
Divisons par Δs2. On peut écrire :
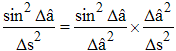
Passons à la limite lorsque tend vers 0 : le premier rapport du second membre tend vers 1, le second membre tend donc vers (dâ/ds)2, carré de la courbure. Quant au numérateur du 1er membre, il devient (αdβ - βdα)2 + (βdγ - γdβ)2 + (γdα - αdγ)2. On le développe en regroupant les dα2, dβ2 et dγ2 et en utilisant que α2 + β2 + γ2 = 1 pour tout s (en tant que cosinus directeurs), on obtient :
(αdβ - βdα)2 + (βdγ - γdβ)2 + (γdα - αdγ)2 = dα2 + dβ2 + dγ2 - (αdα + βdβ + γdγ)2
Or la relation α2 + β2 + γ2 = 1 entraîne la nullité pour tout s de sa différentielle 2αdα + 2βdβ + 2γdγ. Par conséquent :
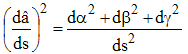
Est-ce bien
K2 = (d2x/ds)2 + (d2y/ds)2 +(d2z/ds)2 ? oui, car on sait que τ(α,β,γ) = dM/ds, donc α = dx/ds, β = dy/ds et γ = dz/ds : K est donc bien la courbure en M(s).➔
Rappelons que la courbure K est l'inverse du rayon de courbure R : K = 1/R et par suite, si R est non nul, n = R.dτ/ds = R.d2M/ds2. Si dτ/ds = K.n est nul (courbure nulle) alors est τ constant : les tangentes en M ont la même direction en tout point de J. L'arc de courbe étant continu, il s'agit d'un segment de droite. Inversement, si M décrit une droite, τ est constant et par suite K = 0|
Interprétation du nombre T défini par db/ds = - T.n : |
db/ds = -
T.n. Par conséquent, en notant b(α',β',γ') :T2 = || db/ds ||2 = (dα
'/ds)2 + (dβ'/ds)2 +(dγ'/ds)2Or, la torsion en un point M(s) est dû/ds, limite du rapport Δ
û/Δs lorsque tend Δs vers 0, Δû désignant l'angle entre les binormales de deux points infiniment proches M(s) et M(s + Δs). Un calcul en tous points semblable au précédent conduirait donc à :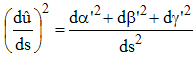
On retrouve bien le nombre T2 : le nombre T est la torsion au point M(s).
➔
Si la torsion T est nulle, alors db/ds = - T.n = 0, donc b est constant : les tangentes en M restent donc parallèles à un plan (P) orthogonal à b. L'arc de courbe étant continu, ces tangentes sont alors nécessairement dans un même plan. Par conséquent, il s'agit d'une courbe plane dans un plan parallèle à (P). Inversement, si M décrit une courbe plane, b est constant et par suite T = 0 : la courbe ne se tord pas, son plan osculateur est fixe.|
Application des formules de Frenet à l'hélice circulaire : |
La courbure et la torsion de l'
hélice circulaire sont constantes et valent, avec les notations ci-dessus, respectivement R/(R2 + λ2) et λ/(R2 + λ2). En effet, on a ici :ds = (R2 + λ2)½ dt, donc s = t.(R2 + λ2)½
τ a pour coordonnées : (-R/(R2 + λ2)½.sin t , R/(R2 + λ2)½.cos t , λ/(R2 + λ2)½).
n a pour coordonnées : (-cos t, -sin t, 0) : normé et colinéaire à d
b =
➔
Avec la définition de l'hélice donnée à la page hélice circulaire, en remarquant que l'on a alors λ = R.tanα, on a les formules :K = cos2α/R et T = sin α.cosα/R