
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
et notion de symétrie centrale |
Voici un motif géométrique. Reproduis-le sachant que :
ABCD est un rectangle » choisis les dimensions comme ci-dessous, mais ce n'est pas une obligation : AB = 17 cm et AD = 7 cm;
I et J sont les milieux de [AB] et [CD] » AIJD et IBCJ sont donc des rectangles (à utiliser par la suite sans explication);
K et L sont les milieux de [AD] et [BC];
[AJ] et [DI] sont les diagonales de AIJD; [IC] et [BJ] sont celles de IBCJ;
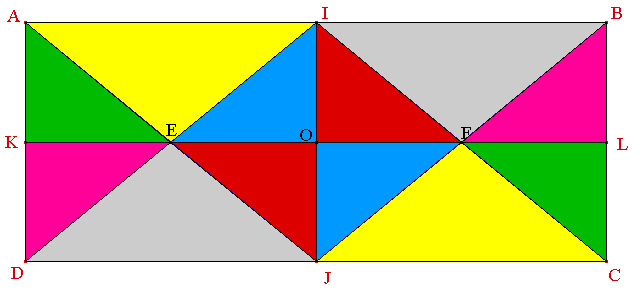
Les triangles jaunes AEI et JFC, par exemple, te paraissent "identiques", on dit plutôt superposables ou isométriques : en "retournant" AEI et en le déplaçant, on pourrait le faire coïncider avec le triangle JFC. Ou encore, on peut penser à faire tourner le rectangle AIOK de 180° autour de O.
Il s'agit plus simplement ici d'une symétrie centrale (de centre O) que tu étudieras en classe de 5ème. Ce type de symétrie est assez rare dans notre environnement. On la rencontre par exemple dans certaines fleurs (marguerite) ou dans les cartes : Valet, Dame, Roi.
Afin de prouver que les triangles AEI et JFC sont superposables, nous allons utiliser deux symétries axiales successives dont les axes sont perpendiculaires :
∗∗∗ Questions ∗∗∗
1/ Recopie (ou imprime l'image) et complète le tableau ci-dessous. Ton professeur te demandera certainement quelques justifications, pour les images de E et F en particulier... Rappelle-toi que la symétrie conserve les distances, les angles, l'alignement, les milieux, ... :
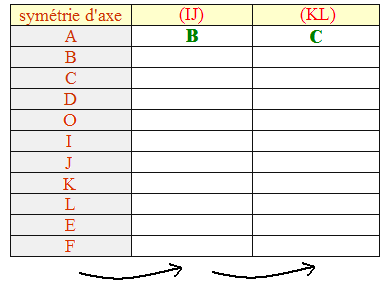
2/ Déduis de ce tableau que les triangles jaunes AEI et JFC sont superposables (côtés et angles de même mesure).
∗∗∗ voir aussi...