ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Polynômes réciproques     Réduction et résolution des équations réciproques de degré pair

Soit P un polynôme de la variable x, à coefficients réels ou complexes de la forme :

P(x) = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₂x² + a₁x + a_o ,

Le polynôme réciproque de P, noté Q ci-dessous, s'obtient en remplaçant les a_k par les a_n-k pour tout k = 0, 1, ..., n :

Q(z) = a_oxⁿ + a₁x^n-1 + a₂x^n-2 + ... + a_n-2x² + a_n-1x + a_n

• Le polynôme réciproque de 5x³ - x² + x - 4 est -4x³ + x² - x + 5.

• Le polynôme réciproque de 5x³ - x² - 4 est -4x³ - x + 5.

• Le polynôme 3x⁴ - 4x³ + 7x² - 4x + 3 est est son propre réciproque.

On déduit immédiatement de la définition que :

Q(x) = xⁿP(1/x)  et, réciproquement... : P(x) = xⁿQ(1/x)

• Si x, non nul, est un zéro de P, alors 1/x est un zéro de Q, et réciproquement.

• On dit qu'un polynôme P est réciproque lorsque P = Q. Auquel cas, pour x ≠ 0, P(x) = 0 ⇔ P(1/x) = 0.

∗∗∗
Montrer que tout polynôme réciproque de degré impair admet -1 comme zéro

Application à la résolution d'une équation réciproque de degré 4 :    

En tant qu'exercice, on apprend au lycée à ramener au degré 2 la résolution d'une équation réciproque de degré 4 en posant X = x + 1/x. Prenons l'exemple de l'équation x⁴ - 2x³ + x² - 2x + 1 = 0 :

• x = 0 n'est pas solution. Mettons x² en facteur, il nous faut résoudre x² + 1/x² - 2(x + 1/x) + 1 = 0.

• On remplace x² + 1/x² par X² - 2, ce qui conduit à l'équation : X² - 2X - 1 = 0 dont les solutions sont 1 ± √2.

• Il nous faut maintenant résoudre x + 1/x = 1 ± √2. Il s'agit de deux équations du second degré en x. Le cas 1 - √2 conduit à un discriminant négatif. Le cas 1 + √2 fournit les deux seules solutions réelles de cette équation dont l'approche graphique est donnée ci-dessous :

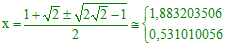
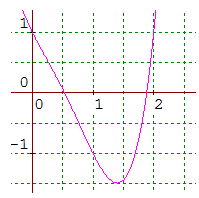
Cas général d'une équation polynomiale réciproque de degré pair :  

D'une façon générale, l'équation algébrique P(x) = 0 où P est un polynôme réciproque de degré pair n = 2p n'admettant pas 0 comme racine (a_o ≠ 0) peut se ramener à une équation de degré p = n/2 d'inconnue X = x + 1/x en mettant x^p en facteur :

P(x) = x^p(a_nx^p + a_n-1x^p-1 + a_n-2x^p-2 + ... + a_n-p + a_n-p-1/x + a_n-p-2/x² + ... + a₁/x^p-1 + a_o/x^p)

P étant réciproque, on a a_k = a_{n - k} pour tout k = 0, 1,2, ... n. Ce qui permet d'écrire :

P(x)/x^p = a_o(x^p +1/x^p) + a₁(x^p-1 +1/x^p-1) + ... + a_p-2(x² +1/x²) + a_p-1(x + 1/x)+ a_p           (3)

En développant A_k = (x + 1/x)^k par la formule du binôme de Newton et en remarquant que le changement de x en 1/x laisse A_k invariant, on peut affirmer que pour tout k, la somme A_k = x^k +1/x^k est un polynôme de degré k en X (on peut aussi procéder par récurrence) :

• X² = (x + 1/x)² = x² + 2 + 1/x², soit  x² + 1/x² = X² - 2;

• X³ = (x + 1/x)³ = x³ + 3x + 3/x + 1/x³, soit x³ + 1/x³ = X³ - 3X;

• X⁴ = (x + 1/x)⁴ = x⁴ + 4x² + 6 + 4/x² + 1/x⁴, soit x⁴ + 1/x⁴ = X⁴ - 4X² + 2;

• ...

L'expression (3) conduit donc à une équation algébrique d'inconnue X de degré n/2. Lorsque X est obtenu, on calcule x en résolvant l'équation du second degré en x : x² - Xx + 1 = 0.