
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
|
La
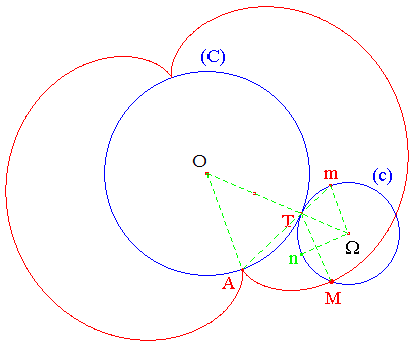
néphroïde est une épicycloïde : elle s'obtient comme lieu d'un point M d'un cercle de rayon r roulant sans glisser à l'extérieur d'un cercle de rayon R = 2r. Une construction assez simple permet de simuler le roulement du cercle (c), A coïncidant avec M au départ. Il s'agit d'obtenir, en termes de longueur d'arc, AT = TM :Allez, roulez...
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération de la
néphroïde. Pour effacer / relancer le lieu :
double-cliquer / cliquer
dans la figure.
Équation générale : »
|
|
|
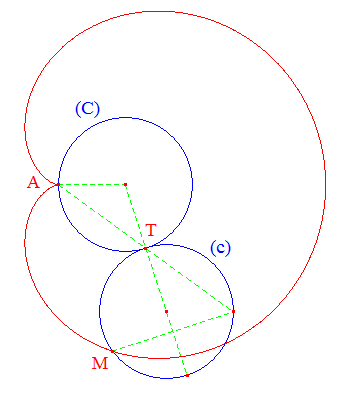
La cardioïde est une épicycloïde : elle s'obtient comme lieu d'un point M d'un cercle de rayon r roulant sans glisser à l'extérieur d'un cercle de rayon R = r. La construction permettant de simuler le roulement du cercle (c) sur C est très simple :
![]()
Si votre navigateur accepte les applets
Java
(»
extension CheerpJ![]() ) :
) :
Génération de la cardioïde.
Déplacer T. Pour effacer / relancer le lieu :
double-cliquer / cliquer
dans la figure.
Équation générale : »