ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Convergence de la série de Riemann dans le cas s réel      par comparaison à une intégrale et par une méthode purement algébrique

Approche analytique :    

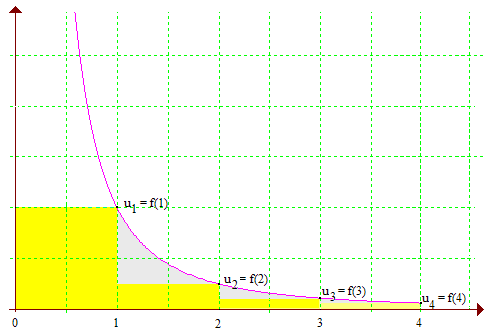
La convergence de la série de Riemann  de terme général 1/n^s (s > 0) s'établit facilement, pour s supérieur à 1, par comparaison à l'intégrale de la fonction f : x → 1/x^s = x^-s sur l'intervalle [1,+∞[. f décroît strictement et on a pour tout p : . L'aire correspondant à la somme de la série est indiquée en jaune.

Par suite :

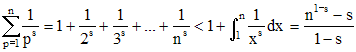
On voit que la série de Riemann converge pour s > 1. La majoration est alors s/(s - 1). Le cas s = 1 est divergent, il correspond à la série harmonique.

 ➔   La somme, lorsqu'elle existe est la célèbre fonction ζ de Riemann dont on soupçonne dans le cas où s est complexe, z = a + bi, de ne posséder que des zéros sur la droite a = 1/2 : c'est la non moins célèbre hypothèse de Riemann.

• Dans le cas s = 2, correspondant à ζ(2) = π²/6 ≅ 1,64, illustré ci-dessus, on trouve que la somme de la série sera inférieure à 2.

Une autre approche : »

• Le cas n = 4, ζ(4) = π⁴/90 ≅ 1,08 est ainsi majoré par 4/3.

Approche algébrique :      

L'étude qui suit est empruntée à un exercice de G. Lefort dans son livre « Algèbre et Analyse, exercices » illustrant le cours de Mathématiques générales de C. Pisot et M. Zamanski, Éd. Dunod, Paris - 1964.

Soit (u_n) une suite numérique positive et décroissante vers 0. On note S_n la somme de ses n premiers termes (n ≥ 1). On pose :

i/  p désignant un entier naturel fixé au moins égal à 1, si  2^p + 1 ≤ n ≤ 2^p+1, on a, par décroissance des u_n :

ii/ Par sommation membre à membre, on a 2^p+1 - (2^p + 1) + 1 = 2^p termes, ce qui conduit à :

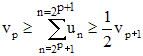
c'est à dire :

iii/ On en déduit les inégalités successives :

et par sommation membre à membre, il vient :

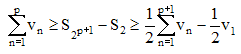
4i/  On voit donc par cette double inégalité, que les Σu_n et Σv_n sont de même nature.

Choisissons alors u_n = 1/n^s, on aura v_n = 2ⁿ × 1/(2ⁿ)^s = 1/(2ⁿ)^s-1 = (1/2^s-1)ⁿ. La suite (v_n) est donc géométrique, de raison 1/2^s-1, convergente (vers 0) pour 1/2^s-1 < 1, soit pour s > 1.

 ➔  Lorsque Σu_n et Σv_n convergent, les encadrements précédents montrent qu'entre la somme S = Σu_n et la somme S' = Σv_n existe la relation :

S₂ + S' ≥ S  ≥  S₂ + (S' - v₁)/2

• Par exemple, dans le cas qui nous intéresse avec s = 2, on a pour n ≥ 1 :  u_n = 1/n², donc v_n = (1/2)ⁿ. S₂ = 1,25, S' = 1 et v₁ = 1/2.
  Ce qui conduit à 2,25 ≥  S ≥ 1,5. Encadrement peu précis, certes, mais qui a le mérite d'exister. On sait que S = ζ(2) = p²/6 ≅ 1,64.

Calcul de ζ(2) = π²/6 ≅ 1,64  : »