
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
@ programme JavaScript utilisable en tant que couple de variables aléatoires (probabilités) » cas d'une série à une variable |
Une série statistique double (X,Y) étant entrée par la donnée de ses couples ({xi} 1≤ i ≤ m ,{yj} 1≤ j ≤ p) et de leurs effectifs ni,j, cette série peut s'interpréter comme la donnée d'un couple de variables aléatoires en considérant les fréquences comme des probabilités : la probabilité du couple (xi ,yj) est ni,j/N où N est l'effectif total de la série double (nombre de couples entrés).
Le tableau statistique entré est généralement rectangulaire : m x p. On pourra tester le programme avec l'exemple simple donné ci-dessous ou avec l'exercice proposé sur la page relative aux couples statistiques.
Le programme calcule :
l'effectif total et la moyenne;
l'écart moyen arithmétique, la variance, l'écart-type;
la covariance;
le coefficient de corrélation linéaire.
Dans ce programme :
nx (resp. ny) le nombre de valeurs observées de X (resp. Y). En déclarant (ligne 12) var eff=new Array(ny), on définit une liste de ny+1 éléments eff[0], eff[1], ..., eff[ny]. En JavaScript les index de tableaux (Array) commencent à 0. Ce rang 0 ne sera pas utilisé.
L'instruction for(i=1;i<=nx;i++){eff[i]=new Array(nx)} (ligne 13) informe le compilateur que chaque élément du tableau précédent est lui-même une liste de nx+1 éléments. En d'autres termes, faisant abstraction des rangs 0, on crée ici une matrice à ny colonnes et nx lignes. On aurait pu préférer nx colonnes et ny lignes. Dans l'exemple ci-dessous, nous avons 6 couples (xi ,yj) : le tableau de leurs effectifs est une matrice 2 x 3 (2 lignes, 3 colonnes) dont les éléments sont eff[i][j].
| xi\ yj | 4 | 5 | 6 | Eff. margi. ni,• |
| 3 | 2 | 5 | 9 | 16 |
| 4 | 3 | 5 | 2 | 10 |
| Eff. margi n•,j |
5 | 10 | 11 | 26 |
Pour info (calcul de la covariance) de l'exemple ci-dessus :
| xiyj | 12 | 15 | 18 | 16 | 20 | 24 | Σ |
| ni,j | 2 | 5 | 9 | 3 | 5 | 2 | 26 |
| xiyj.ni,j | 24 | 75 | 162 | 48 | 10 | 48 | 367 |
Réponses du programme concernant cet exemple :
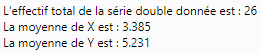
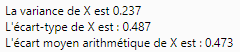
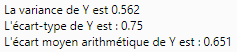

<SCRIPT
LANGUAGE=JavaScript>
var x=new Array(), y=new Array(),eff_margi_x=new Array(),eff_margi_y=new Array()
function stat_deux() // programme stat deux
variables
{
nx="";ny=""
nx=eval(prompt("Entrez le cardinal de la série X :",nx))
if (nx==null) {return}
ny=eval(prompt("Entrez le cardinal de la série Y :",ny))
if (ny==null) {return}
a="o";equi=1;
a=prompt("Pondération = 1 ? (o/n)",a)
// pondération = 1 ?
if (a==null) {return} else {if(a=="n"){equi=0}};
var eff=new Array(ny)
// ligne 9
for(i=1;i<=nx;i++){eff[i]=new Array(nx)}
// ligne 10
eff_t=0;test_y=0
// entrée des couples
for(i=1;i<=nx;i++)
{
a="";a=prompt("Entrez x("+i+"):",a)
if (a==null) {return} else {x[i]=eval(a)};
for(j=1;j<=ny;j++)
{
if(test_y==0) // les valeurs de Y ne sont
demandées qu'une seule fois (lorsque i = 1)
{b="";b=prompt("Entrez y("+j+"):",b)
if (b==null) {return} else {y[j]=eval(b)}
}
else
{b=y[j]}
e="";e=eval(prompt("Donnez maintenant l'effectif du couple ("+a+","+b+") :",e))
if (eff==null) {return} else {eff[i][j]=e;eff_t=eff_t+e}
} // fin boucle j
test_y=1;
} // fin boucle i
for(i=1;i<=nx;i++) // eff marginaux X
{
eff_margi_x[i]=0
for(j=1;j<=ny;j++)
{
eff_margi_x[i]=eff_margi_x[i]+eff[i][j]
}
}
for(j=1;j<=ny;j++) // eff marginaux Y
{
eff_margi_y[j]=0
for(i=1;i<=nx;i++)
{
eff_margi_y[j]=eff_margi_y[j]+eff[i][j]
}
}
moy_x=0; //calcul de E(X)
for(i=1;i<=nx;i++)
{
moy_x=moy_x+eff_margi_x[i]*x[i]
}
moy_x=moy_x/eff_t;
moy_x_arr=sign(moy_x)*Math.floor(Math.abs(moy_x)*1000+0.5)/1000
// arrondi au milllième
moy_y=0; //calcul de E(Y)
for(j=1;j<=ny;j++)
{
moy_y=moy_y+eff_margi_y[j]*y[j]
}
moy_y=moy_y/eff_t;
moy_y_arr=sign(moy_y)*Math.floor(Math.abs(moy_y)*1000+0.5)/1000
// arrondi au milllième
alert("L'effectif total de la série double donnée est : "+eff_t+"\n"+"La moyenne
de X est : "+moy_x_arr+"\n"+"La moyenne de Y est : "+moy_y_arr)
em=0;Vx=0; //calcul écart moyen
arithmétique, V(X) et écart-type
for(i=1;i<=nx;i++)
{
em=em+eff_margi_x[i]*Math.abs(x[i]-moy_x);
Vx=Vx+eff_margi_x[i]*x[i]*x[i]
}
Vx=Vx/eff_t-moy_x*moy_x;sx=Math.sqrt(Vx);em=em/eff_t;
V_arr=Math.floor(Math.abs(Vx)*1000+0.5)/1000 //
arrondi au milllième
s_arr=Math.floor(Math.abs(sx)*1000+0.5)/1000
em_arr=Math.floor(Math.abs(em)*1000+0.5)/1000
alert("La variance de X est "+V_arr+"\n"+"L'écart-type de X est : "+s_arr+"\n"+"L'écart
moyen arithmétique de X est : "+em_arr)
em=0;Vy=0; //calcul écart moyen
arithmétique, V(Y) et écart-type
for(j=1;j<=ny;j++)
{
em=em+eff_margi_y[j]*Math.abs(y[j]-moy_y);
Vy=Vy+eff_margi_y[j]*y[j]*y[j]
}
Vy=Vy/eff_t-moy_y*moy_y;sy=Math.sqrt(Vy);em=em/eff_t;
V_arr=Math.floor(Math.abs(Vy)*1000+0.5)/1000
// arrondi au milllième
s_arr=Math.floor(Math.abs(sy)*1000+0.5)/1000
em_arr=Math.floor(Math.abs(em)*1000+0.5)/1000
alert("La variance de Y est "+V_arr+"\n"+"L'écart-type de Y est : "+s_arr+"\n"+"L'écart
moyen arithmétique de Y est : "+em_arr)
moy_xy=0; // calcul
de la covariance = E(XY) - E(X)E(Y) et du coeff de corrélation
for(i=1;i<=nx;i++)
{
for(j=1;j<=ny;j++)
{
moy_xy=moy_xy+x[i]*y[j]*eff[i][j]
}}
moy_xy = moy_xy/eff_t;
cov_xy=moy_xy-moy_x*moy_y
cov_xy_arr=sign(cov_xy)*Math.floor(Math.abs(cov_xy)*1000+0.5)/1000
// arrondi au milllième
r=cov_xy/(sx*sy);
r_arr=sign(r)*Math.floor(Math.abs(r)*1000+0.5)/1000
a$="Faible présomption de linéarité entre X et Y."
if(Math.abs(r)>=0.866)
{a$="Forte présomption de linéarité entre X et Y."}
alert("La covariance de (X,Y) est "+cov_xy_arr+"\n"+"Le coefficient de
corrélation est : "+r_arr+"\n"+a$);
} // fin stat_deux()
function sign(x) // le signe de x est 1 si
positif, 0 si nul, -1 si négatif
{
if(x==0){return 0} else {if (x>0) {return 1} else {return -1}}
}
</SCRIPT>