ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Apprendre à construire : perpendiculaires et symétrie axiale     niveau CM2/6ème

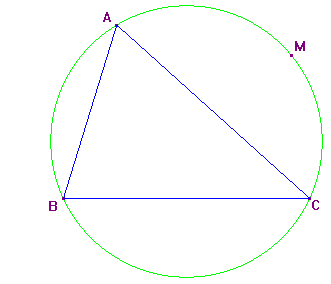
♦ 1ère étape : reproduis la figure ci-dessus en traçant :

• un cercle de 8 cm de diamètre;
• une corde [BC] de 7 cm;
• le triangle ABC de sorte que AB = 5,5 cm.

♦ 2ème étape : complète la figure en traçant :

• 1. la perpendiculaire au côté [BC] passant par A (hauteur issue de A);
• 2. la perpendiculaire au côté [AC] passant par B (hauteur issue de B);
• 3. le symétrique de M par rapport à la droite (BC);        ← clique sur symétrique pour un rappel
• 4. le symétrique de M par rapport à la droite (AC);
• 5. le symétrique de M par rapport à la droite (AB);

♦ 3ème étape : appelle H le point d'intersection des deux perpendiculaires tracées en 1. et 2. Observe bien la figure : que peux-tu dire du point H et des trois symétriques ?

Si (d) est une droite et A un point quelconque non situé sur (d), on dit que :

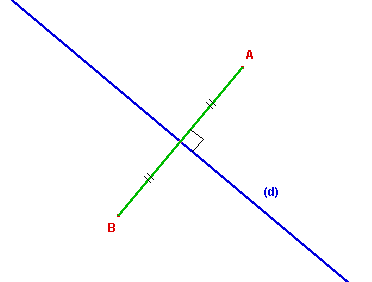
 ➔   Si A est situé sur (d), le symétrique de A est A lui-même.

Avec le vocabulaire de la médiatrice d'un segment, droite perpendiculaire à ce segment et passant par son milieu :

Si ton navigateur accepte les applets Java :
Tu peux déplacer A;  tu peux aussi déplacer la droite.