ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Les clés de la construction de Napoléon : construire l'inverse de     l'inverse du centre cherché       »  inversion géométrique

 ➔  Cette étude établissant la source de la construction au compas seul du centre d'un cercle donné, dite construction de Napoléon, est due à Frédéric Gorgori, professeur de mathématiques.

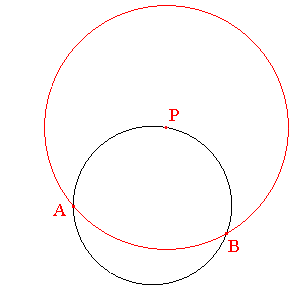
Le cercle noir, que l'on nommera (n), est le cercle dont on cherche à construire le centre "perdu". Soit P un point quelconque du cercle et (r) un cercle de centre P, tracé en rouge, nommé (r), coupant (n) en A et B.

P1.  Tout cercle (C) de rayon R, de centre J définit une inversion de pôle J, de puissance √R dont (C) est l'ensemble des points invariants : » inversion géométrique

Considérons l'inversion φ de pôle P dont (r) est l'ensemble des points invariants.

P2.  L'inverse d'un cercle (c) passant par le pôle O d'inversion est une droite   » inversion Th.2

Notre cercle (n) passant par le pôle P. Selon P2, son inverse est donc une droite. Or, A et B sont invariants en tant que points de (r) : l'inverse de (n) par φ est la droite (AB).

P3.  Dans une inversion transformant un cercle (c) en une droite (d), le centre de (c) et le symétrique du pôle par rapport à (d) sont inverses l'un de l'autre : » inversion Th.3

Soit O' le symétrique de P par rapport à (AB). Ce symétrique est facilement constructible au compas seul au moyen de deux cercles de centre A et B passant par P :  » symétrie axiale

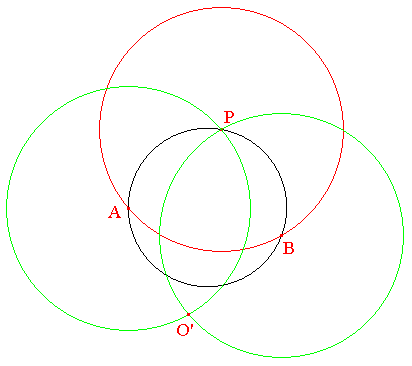
L'inverse de (n) est (AB) et, selon P3, le centre O de (n) est l'inverse de O', symétrique du pôle P par rapport à (AB).

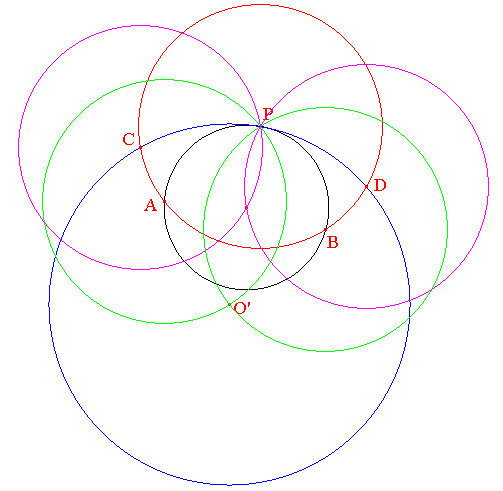
Pour conclure, il nous faut donc à présent construire φ(O') = O au compas seul. Pour cela, faisons de O' le centre d'un cercle qui se transforme en une droite par l'inversion φ : selon P2, il suffit de faire passer ce cercle par P : nommons-le (b), en bleu ci-dessous. Il coupe (r) en C et D invariants par φ : l'inverse de (b) est la droite (CD).

Appliquons de nouveau P3 : le centre de (b) et le symétrique P' de P par rapport à (CD) sont inverses l'un de l'autre. C'est dire que O' = φ(P'), or φ(O') = O, donc, en appliquant φ,  O = P' (involution) :

Le point O s'obtient donc maintenant très facilement comme symétrique de P par rapport à (CD) à l'intersection, autre que P, des deux cercles roses ci-dessous.

On comprend mieux ainsi la présence des nombreux cercles dans la fameuse construction de Napoléon
qui peuvent sembler, a priori, tirés d'un chapeau...

Merci à Frédéric Gorgori pour cette belle justification.