ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Construction au compas seul du milieu M d'un segment        » Carré et compas seul , une construction à la règle seule

La construction au seul compas du symétrique A' de A par rapport à un point 0 est relativement simple. Elle revient à la construction partielle de l'hexagone régulier de centre O, dont les côtés mesurent OA.

Le mathématicien danois Georg Mohr se passionna pour ce type de problème. On trouvera à la page qui lui est consacrée la construction du symétrique d'un point. Plus difficile est la construction, au seul compas, du milieu M d'un segment [AB] :

Construction, au seul compas, du milieu d'un segment :    

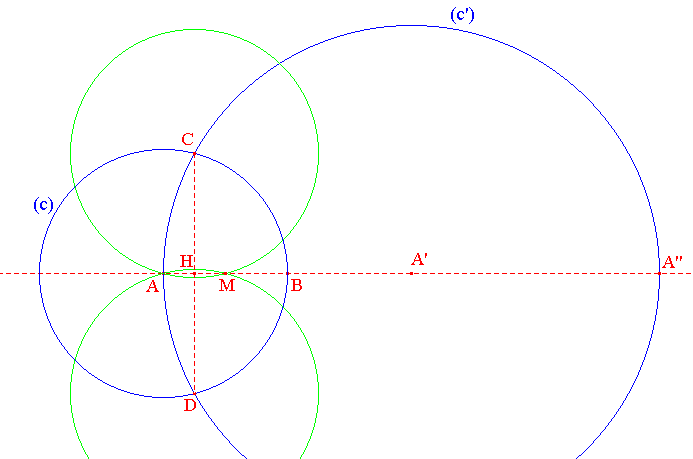
On construit tout d'abord le symétrique A' de A par rapport à B comme indiqué ci-dessus. On trace :

• le cercle (c) de centre A passant par B

• le cercle (c') de centre A' passant par A. Ces cercles se coupent en C et D.

• Les cercles de centres C et D passant par A se recoupent au point M, milieu de [AB].

Preuve :    

par construction, la figure admet (AB) comme axe de symétrie. C'est dire que M est aligné avec A et B. Le segment [AA"] étant un diamètre de (c'), ACA" est rectangle en C. [CH] est la hauteur relative à l'hypoténuse. On a donc (relation élémentaire dans un triangle rectangle) :

»  Napoléon , Mascheroni                         Perpendiculaire et règle seule : »

 ➔   Pour en savoir plus :

• Théorie des corps, la règle et le compas, par Jean-Claude Carrega, Ed. Hermann, 1989.

• Le site de Jen-chung Chuan, nombreux exemples :
  - Constructions au compas seul : http://poncelet.math.nthu.edu.tw/chuan/compass-only/compass-only.html
  - Constructions à la règle seul : http://poncelet.math.nthu.edu.tw/chuan/ruler-only/ruler-only.html