ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Décomposition d'une fraction
en somme de
2, 3, 4 ou 5 fractions unitaires |
Pour les amateurs de décomposition de fractions en fractions unitaires, voici un programme JavaScript susceptible de décomposer une fraction en une somme de 2, 3, 4 ou 5 fractions unitaires chères au scribe égyptien Ahmes.
Rappelons que le mathématicien américain Solomon W. Golomb (1932-), professeur à l'université Los angeles (USC, University of Southern California) prouva (An algebraic algorithm for the representation problems of the Ahmes papyrus,1962) que :
Toute fraction
irréductible n/d peut se décomposer en une somme d'au plus
n fractions unitaires distinctes
Cas 2/d irréductible : on pose d = ab avec a et b impairs) et, éventuellement, a = 1 si d est premier ou un carré parfait; on a alors 2/ab = 1/ka + 1/kb avec k = (a+b)/2 et ka distinct de kb. Par exemple, 2/17 = 1/9 + 1/153. Le cas 1/17 + 1/17 est trouvé par l'ordinateur mais considéré ici comme trivial : on recherche des fractions distinctes 2 à 2.
Cas 3/d irréductible : on écrit 3/d = 1/d
+ 2/d et on applique la transformation précédente :
3/d = 1/d + 1/ka + 1/kb.
➔ Les cas n/d avec n > 3 sont plus subtils... Pour n = 4 et n = 5 on se rendra sur la page des conjectures d'Erdös et de Sierpinski.
| Programme JavaScript : |
Le programme listé ci-dessous simplifie si possible tout d'abord la fraction (division par le pgcd). Si x = a/n avec a > n, le programme calcule le quotient et le reste de la division euclidienne puis décompose r/n.
Par défaut, l'ordinateur choisit 100 pour le maximum des valeurs prises par x, y, z, t et u. Si aucune solution n'apparaît, augmentez progressivement ce choix ou le nombre de fractions si vous êtes convaincu de l'existence d'une solution. Au-delà de 3 fractions, les temps de calcul peuvent être très longs (plusieurs millions d'essais) !
! L'ordinateur vous mettra en garde périodiquement si les temps de
calculs lui paraissent trop longs
!
Par exemple, il ne serait pas très pertinent de chercher à décomposer
4/9 en somme de 5 fractions unitaires...
Exemples d'exécution :
|
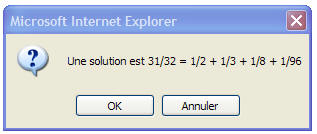
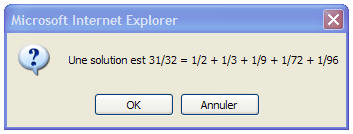
<SCRIPT
LANGUAGE=JavaScript> switch(nf) // début des calculs{ case 2: for(x=1;x<=max;x++) { for(y=x;y<=max;y++) { if(a*x*y==n*(x+y)){u=fin2();if(u==0)return} } } alert("Pas (plus) de solutions avec Max = "+max) break; case 3: for(x=1;x<=max;x++) { for(y=x;y<=max;y++) { for(z=y;z<=max;z++) {if(a*x*y*z==n*(x*y+y*z+x*z)){u=fin3();if(u==0)return} } } } alert("Pas (plus) de solutions avec Max = "+max) break; case 4: for(x=1;x<=max;x++) { for(y=x;y<=max;y++) { for(z=y;z<=max;z++) { for(t=z;t<=max;t++) { if(a*x*y*z*t==n*(x*y*z+y*z*t+x*z*t+x*y*t)){u=fin4();if(u==0)return} } } } } alert("Pas (plus) de solutions avec Max = "+max) break; case 5: for(x=1;x<=max;x++) { for(y=x;y<=max;y++) { for(z=y;z<=max;z++) { for(t=z;t<=max;t++) { for(u=t;u<=max;u++) { if(a*x*y*z*t*u==n*(x*y*z*t+y*z*t*u+x*z*t*u+x*y*t*u+x*y*z*u)){u=fin5();if(u==0)return} } } } } } alert("Pas (plus) de solutions avec Max = "+max) break; default: alert("Fatal error, désolé, cas non prévu") } // --------------------------------------------------fin switch } // --------------------------------------------------fin go() function pgcd(a,b) { if (b==0) {return a} else {return pgcd(b,a%b)} } //---------------------------------------------------------------------- function fin2() { if(!confirm("Une solution est "+a+"/"+n+" = 1/"+x+" + 1/"+y)){return 0} else {return 1} } function fin3() { if(!confirm("Une solution est "+a+"/"+n+" = 1/"+x+" + 1/"+y+" + 1/"+z)){return 0} else {return 1} } function fin4() { if(!confirm("Une solution est "+a+"/"+n+" = 1/"+x+" + 1/"+y+" + 1/"+z+" + 1/"+t)){return 0} else {return 1} } function fin5() { if(!confirm("Une solution est "+a+"/"+n+" = 1/"+x+" + 1/"+y+" + 1/"+z+" + 1/"+t+" + 1/"+u)){return 0} else {return 1} } </SCRIPT> |