
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
|
➔ on ne traite ici que le cas très particulier de la conjecture où le triangle est équilatéral.
On considère un triangle équilatéral ABC et un point M intérieur à ce triangle (éviter a priori de le placer sur un de ses axes de symétrie).
On note H, K et L les projections orthogonales de M sur les côtés du triangle.
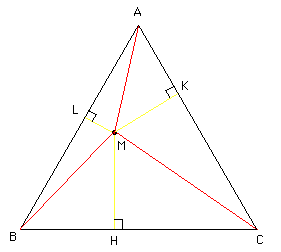
MA + MB + MC ≥ 2 × (MH + MK + ML)
On sait que les médianes d'un triangle se coupent au tiers à partir de leur pied. Donc, si M est l'orthocentre, également centre de gravité (à droite), on a clairement l'égalité voulue puisque :
MA = 2MH , MB = 2MK et MC = 2ML
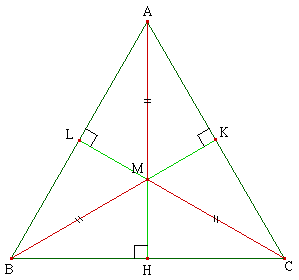
Supposons maintenant M autre que O, orthocentre et centre de gravité du triangle (dessin ci-dessous). ABC étant équilatéral, on a, selon le théorème de Viviani pour tout point M :
MH + MK + ML = AH (hauteur du triangle)
La conjecture étudiée devient alors :
On montre facilement, qu'à l'exception de O, aucun point M situé sur l'un des axes de symétrie, (AH) par exemple, ne convient en étudiant la fonction
lorsque M(0,y), identifié à son ordonnée y, décrit [AH] dans un repère orthonormé d'origine H dont les axes sont dirigés par [HB) et [HA) : f atteint son unique minimum en O, orthocentre et centre de gravité du triangle ABC.
Si on pose HB = a, on a HA = a√3 et MA + MB + MC = f(y) = a√3 - y + 2√(a2 + y2). Le minimum de d est atteint en en y = a/√3, soit au tiers de HA. Soit maintenant M, non situé sur un des axes de symétrie. L'ellipse de foyers B et C, passant par M, coupe [AH] en J.
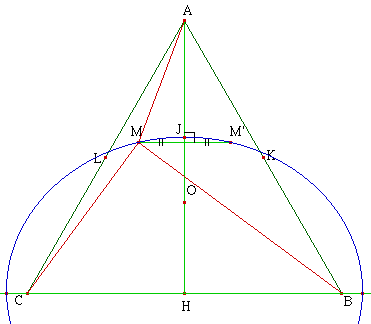
Par définition bifocale de l'ellipse, on a JB + JC = MB + MC et par convexité de cette courbe : AJ < AM. Par suite :
MA + MB + MC > JA + JB + JC
J étant situé sur [AH], on a JA + JB + JC ≥ 2AH et donc, a fortiori : MA + MB + MC > 2AH. La conjecture d'Erdös, dans le cas équilatéral est donc prouvée.