ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
 Cochléoïde
» du latin
cochlea
= limaçon et du grec
eïdos =
forme |
L'équation (coordonnées polaires) de cet escargot est :
Le changement de t en -t n'affecte pas r. La courbe est donc symétrique par rapport à l'axe des abscisses.
La courbe s'enroule autour de l'origine car sin t reste bornée en oscillant entre - 1 et +1 et sin(t)/t tend donc vers 0 lorsque t augmente en valeur absolue.
La cochléoïde apparaît comme la projection conique (projection centrale) d'une hélice circulaire lorsque le centre de la projection est choisi sur cette dernière :
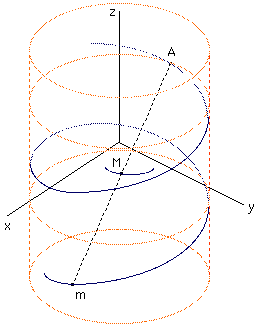Dans un repère
orthonormé (0,x,y,z), l'équation
de l'hélice d'axe Oz
le long d'un cylindre de rayon R, est de la forme :
Choisissons comme centre de la projection conique le point A(0, R, aπ/2) correspondant à t = π/2. Notons m(x,y,z) un point de l'hélice et M le point projeté sur le plan xOy.
Pour chaque t, la droite (Am) est dirigée par (Rcos t , R(sin t - 1), at - aπ/2) et pour tout point M(X,Y,Z) de (Am), on peut alors s'écrire :
X = λRcos t
Y - R = λR(sin t - 1)
Z - aπ/2 = λa(t - π/2)
Le point projeté M(X,Y,Z) est défini par Z = 0 donc par λ(π/2 - t) = π/2. D'où :
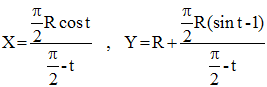
En savoir plus sur les coordonnées paramétriques : »
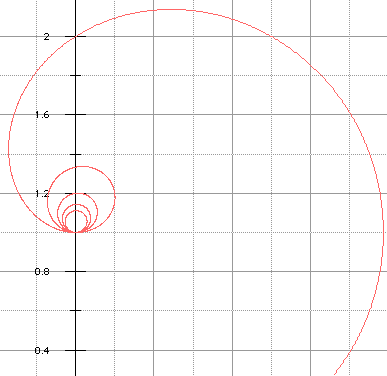
Le tracé de cette courbe ressemble bigrement à une cochléoïde. Montrons-le :
A une translation près, en retirant R à Y, puis en choisissant R tel que Rπ/2 = 1 (homothétie) et en posant enfin θ = π/2 - t, il vient :
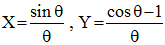
par symétrie (isométrie) par rapport à (OX), on peut remplacer par :
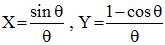
ou encore :
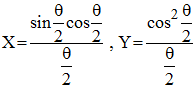
Passons en coordonnées polaires r = f(T) avec T = π/2 - θ/2. On doit avoir X = rcosT et Y = rsinT. Ceci est loisible avec :
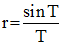
C'est bien le résultat cherché.
∗∗∗
Projection orthogonale plane d'une hélice circulaire