ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges
  Cubique de Tschirnhausen
et trisectrice de Catalan
» trisection de l'angle |
Comme expliqué sur la page cubique de Tschirnhausen, la parabole est la podaire de cette cubique par rapport à son foyer F, c'est à dire l'ensemble des points M qui sont les pieds des perpendiculaires menées de F aux tangentes à la cubique.
Quand T décrit la cubique que nous notons (c), on a ^FMK = ^KMx' = ^MKF : MFK est isocèle en F.
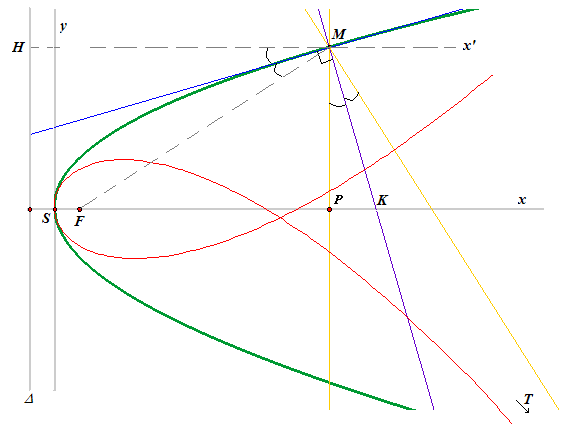
Attachons-nous à la figure ci-dessous (mêmes notations) où le point T est atteint. Le triangle FMT étant rectangle en M, le milieu J de l'hypoténuse vérifie JF = JM : les angles ^JFM et ^FMJ ont même mesure.
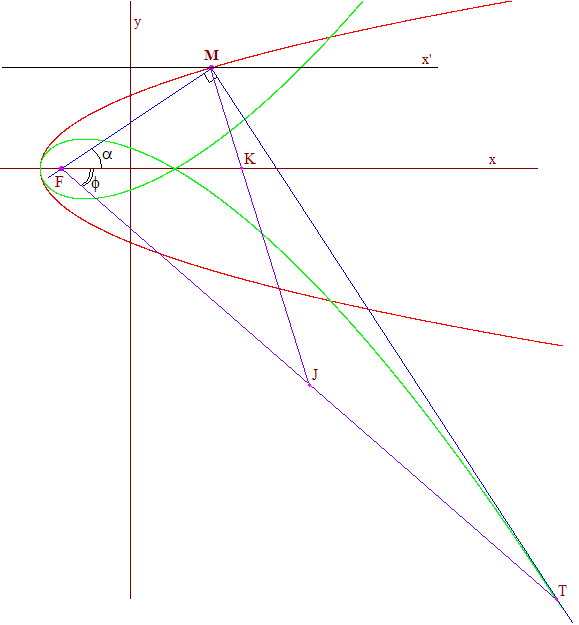
Soit α l'angle ^MFK et Φ l'angle ^TFK. On a ^FMK = ½(π - α). On a donc : ^FMK = ^FMJ = ^MFJ = α + Φ. On en déduit l'égalité :
3α = π - 2Φ, ou en degrés : 3α = 180° - 2Φ , ou encore : Φ/3 = 30° - α/2
Par conséquent, un angle aigu de mesure Φ étant donné, on place T sur la cubique afin que ^xFT = Φ. La tangente en T fournit M, puis l'angle α = ^MFx. On construit la bissectrice de ^MFx. On a alors construit α/2. Il faut retirer 30° (π/6). Or 30° est constructible : c'est la trisection de l'angle droit.