Calcul élémentaire de e

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Calcul élémentaire du nombre e
@ Calcul précis par la formule d'Euler-Maclaurin , calcul haute précision...

On se propose de calculer au moyen de l'ordinateur une valeur approchée du nombre e, base des logarithmes népériens. La première est élémentaire et peu précise. La seconde fournit 15 décimales, ce n'est pas si mal. On trouvera beaucoup mieux ici...

Méthode 1 :

En dehors d'un encadrement simple de e, une première méthode rustique n'utilisant que des connaissances élémentaires, niveau terminale des lycées, consiste à évaluer avec une simple calculatrice ou un ordinateur le nombre (1 + 1/n)ⁿ pour n suffisamment grand. En effet, on sait que :

car cette limite n'est autre que le nombre dérivé en x = 0 de la fonction f(x) = ln(1 + x).

En posant x = 1/n, on en déduit une formule pressentie par Neper et établie rigoureusement par Euler :

Programmation de la méthode en JavaScript

Le premier programme ne fait volontairement pas appel à la fonction puissance car, dans les langages de programmation, cette dernière utilise généralement xⁿ = e^{n.ln x} : on tourne en rond !
Le second programme utilise la fonction puissance du langage JavaScript : l'instruction Math.pow(x,n) calcule xⁿ. Mais pour x² et x³, utiliser plus simplement x*x et x*x*x. » fonctions mathématiques usuelles

<SCRIPT LANGUAGE=JavaScript>
function expo1()
{
n=10000 ; n=eval(prompt("n = ",n))
e=1 ; f=1+1/n;
for(k=1;k<=n;k++) {e=e*f} // on calcule fⁿ
alert("e = "+e)
}

function expo2()
{
n=10000 ; n=eval(prompt("n = ",n))
e=Math.pow(1+1/n,n)
alert("e = "+e)
}

</SCRIPT>

➔ Remarquer que n = 10 000 ou 100 000 ne procurent que 3 décimales exactes. Il y a accumulation des erreurs d'arrondi. Le procédé est peu efficace (les décimales soulignées sont fausses).

Pour n = 10000, on obtient e ≅ (1,0001)¹⁰⁰⁰⁰ = 2,7181459...
Pour n = 1 000 000 : e ≅ (1,000001)^1000000 = 2,71828137...
Avec une calculatrice, type collège/lycée (séquence de touches) : 1 + 10000 1/x = y^x10000 = 2,71814...

Méthode 2 :

Au moyen de la formule de Taylor, établir le développement en série du nombre e (dit parfois développement de Euler ) est évident. Nous allons cependant utiliser un détour plus formateur lié à la formule de Maclaurin pour les polynômes : si P est un polynôme de degré n :

P(x) = a_nxⁿ + a_n-1x^n-1+ ... + a₂x² + a₁x + a_o

Notons P⁽ⁱ⁾ le polynôme dérivé ième de P : P' = P⁽¹⁾, P" = (P')' = P⁽²⁾, etc. On a alors :

P(0) = a_o, P'(0) = a₁, P"(0) = P⁽²⁾(0) = a₂.2! , P⁽³⁾(0) = a³.3!, ... , P⁽ⁿ⁾(0) = a_n.n!

et pour k > n : P^(k)(0) = 0.

On en déduit la formule suivante, dite de Taylor / Maclaurin pour les polynômes :

P(x) = P(0) + x.P'(0) + x².P"(0)/2! + x³.P⁽³⁾(0)/3! + xⁿ.P⁽ⁿ⁾(0)/n!

Généralement, dans le cas d'une fonction indéfiniment dérivable f(x), aucune dérivée f^(k)n'est la fonction nulle. Ecrivons alors :

f(x) = f(0) + x.f

'(0) + x².f

"(0)/2! + x³.f⁽³⁾(0)/3! + xⁿ.f ⁽ⁿ⁾(0)/n! + R_n(x)

en espérant que si n est suffisamment grand, le reste R_n(x) puisse être considéré comme "suffisamment petit". Dans le cas de notre fonction exponentielle, vu que f(x) = f'(x) = e^xpour tout réel x, il apparaît immédiatement que, pour tout x :

R_n(x) > 0 et : R_n(x) - R'_n(x) = - xⁿ/n!

Nous sommes en présence d'une équation différentielle linéaire du 1er ordre avec second membre :

y - y' = - xⁿ/n!

La solution générale de l'équation homogène est y = Ke^x.Recherchons alors la solution générale en posant y = z.e^x (méthode de la variation de la constante). En utilisant que e^o= 1, on obtient facilement :

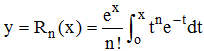
On sait (cf. encadrement élémentaire de e) que 2 < e < 3. Choisissons alors x = 1 et majorons R_n(1) en remarquant que sur l'intervalle [0,1] d'intégration, on a 0 < e^-t ≤ 1. Il vient :

e = 1 + 1/1! + 1/2! + 1/3! + ... + 1/n! + R_n(1) avec 0 < R_n(1) < 3/(n + 1)!

Cette majoration du reste est très intéressante, voire indispensable : elle permet d'apprécier facilement l'erreur commise en tronquant le développement de e à l'ordre n.

On note en passant :

e^x = 1 + x + x²/2! + x³/3! + ... + xⁿ/n! + ...

» Euler Un autre calcul de majoration de l'erreur commise : »

Programmation de la méthode en JavaScript

<SCRIPT LANGUAGE=JavaScript>
function mac()
{
e=1 ; fac=1;
for(n=1;n<=30;n++)
{fac=fac*n ; e=e+1/fac ; er=3/fac/(n+1);
if (n%6==0)
{
if(!confirm("n = "+n+" e = "+e+"\n"+"erreur< "+er)) return
}
}
}
</SCRIPT>

➔ l'instruction n%6 retourne le reste de la division euclidienne de n par 6 : on affiche les résultats partiels si n est multiple de 6. La double égalité == est l'égalité conditionnelle. Écrire if(n%6=0) est incorrect en JavaScript.

» fonctions mathématiques usuelles

if(!confirm(message) return exprime que si l'utilisateur clique sur le bouton "Annuler", le programme est arrêté.
D'une façon générale, en JavaScript , le ! (point d'exclamation) exprime la négation : if(!confirm(...) ⇔ si on ne confirme pas(...)

Résultat :

n = 30 : e = 2,7182818284590455
erreur < 3.648375124660554e-34, c'est à dire environ 3,6 × 10^-34.

En fait, il est illusoire de dépasser n = 18 car dès que R_n sera inférieur à 10^-16, le calcul "piétinera", ce que confirme l'exécution du programme : l'ordinateur travaillant avec 16 décimales, la dernière n'est pas assurée (arrondi probable). D'ailleurs, un calcul plus précis montre que le dernier 5 est en fait un 2 :

e = 2,718 28 18 28 45 90 45 23536...

» Un calcul haute précision...