Bifolium

ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Bifolium asymétrique » interprétation géométrique , bifolium symétrique

Cette courbe possède deux "feuilles" asymétriques. Son équation en coordonnées polaires est de la forme :

r = (a.cos t + b.sin t)cos² t

La courbe admet en l'origine un point triple qui est un point de rebroussement en π/2.

en t = 0, on a r = 1, "point de départ" de la courbe.

t varie théoriquement sur l'intervalle [0,2π]. Mais r(t + π) = - r(t) : la courbe est donc obtenue entièrement en faisant varier t sur l'intervalle [0,π].

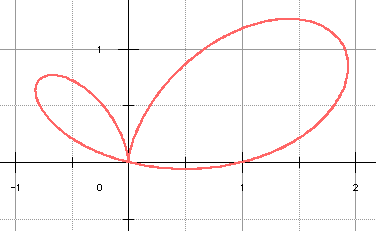
Ci-dessus : a = 1, b = 4

Le bifolium asymétrique est une courbe algébrique de degré 4 (quartique) : en effet, en passant aux coordonnées paramétriques, on a :

x = r.cos t = cos³(t)[a.cost + b.sin(t)]
y = r.sin t = cos²(t)sin(t)[a.cost + b.sin(t)]
x² + y² = cos⁴(t)[a.cost + b.sin(t)]²
(x² + y²)² = x²cos²(t)[a.cost + b.sin(t)]²
= x² x [a.cos³t(a.cos t + b.sin t) + b.sin t.cos²t(a.cos t + b.sin t)]

On constate que l'on retrouve ax + by dans le crochet. En définitive, le bifolium asymétrique est, comme le bifolium symétrique, une quartique bicirculaire dont une équation est de la forme :

(x² + y²)² - x²(ax + by) = 0

Une interprétation géométrique de cette courbe :

Dans un repère orthonormé, considérons les points A(a,0) et B(a,b). Soit C un point du cercle (c) de diamètre [OB]. Soit H le projeté orthogonal de C sur l'axe des abscisses et M le projeté orthogonal de H sur (OC).

Quel est l'ensemble des points M lorsque C décrit (c) ?

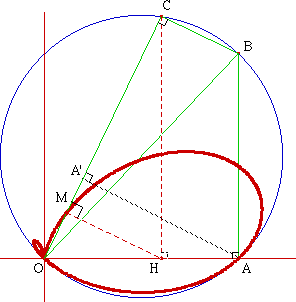
Posons ^AOC = t. On a, en mesure algébrique :

OM = OH.cos t = OC.cos²t

et si A' est le projeté orthogonal de A sur (OC), il vient :

OA' = a.cos t et A'C = b.sin t car B se projette en C et (AB)// (CH)

Donc, en coordonnées polaires :

r = OM = (a.cos t + b.sin t).cos²t

M décrit donc le bifolium asymétrique étudié ci-dessus. La petite boucle est ici très petite car a est numériquement proche de b.

» folium simple, bifolium, folium de Descartes, quadrifolium