
ChronoMath,
une chronologie des MATHÉMATIQUES
à l'usage des professeurs de
mathématiques, des étudiants et des élèves des lycées & collèges
Le mathématicien suisse
Gabriel Cramer fait état de cette courbe
(1750) dans son
« Introduction à l'Analyse des lignes courbes algébriques » :
Dans un repère
orthonormé (Ox,Oy), considérons un cercle (c) passant par
l'origine et les point A(a,0) et B(0,b) de ce cercle. A tout point P de (c), on
associe le point M de même ordonnée et dont l'abscisse
est la distance OP.
Le point M, ainsi défini géométriquement
décrit le lieu en rouge ci-dessous, obtenu avec Cabri-Géomètre
II (a > 0, b < 0) :
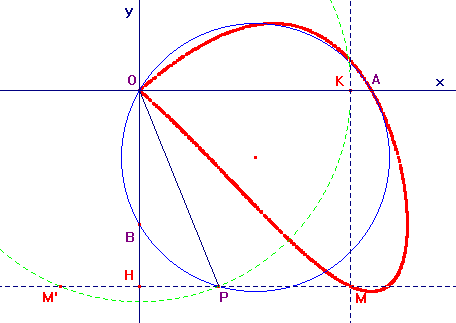
Le cercle (OAB) est centré en J(a/2,b/2), milieu de
[AB] et son équation cartésienne peut s'écrire : (x - a/2)2 + (y -
b/2)2 = r2. AB est un
diamètre, on a donc 4r2 = (a2 + b2)
et, après simplification, l'équation du cercle devient x2 + y2 = ax + by ≥ 0. Notons
alors X et Y les coordonnées de M; on a Y = y et X2 = OP2
= x2 +
y2 = ax + bY. Par suite : (X2 - bY)2
= a2x2 = a2(X2 -
Y2). D'où l'équation
cartésienne :
(X2 - bY)2
= a2(X2 - Y2)
Sous cette forme, le passage au carré de X fait
oublier que, par définition X est positif. Mais
considérons le point M' symétrique de M par rapport
à Oy : on a xM'= -X et yM' = Y et la
courbe, réunion des lieux de M et M', vérifie
l'équation ci-dessus.
➔
La besace est
ainsi une courbe
algébrique
(fermée) du 4ème degré : c'est une
quartique. Le nom de besace
lui fut donné car elle ressemble alors à un tel petit
sac à deux poches que l'on portait autour de la ceinture.
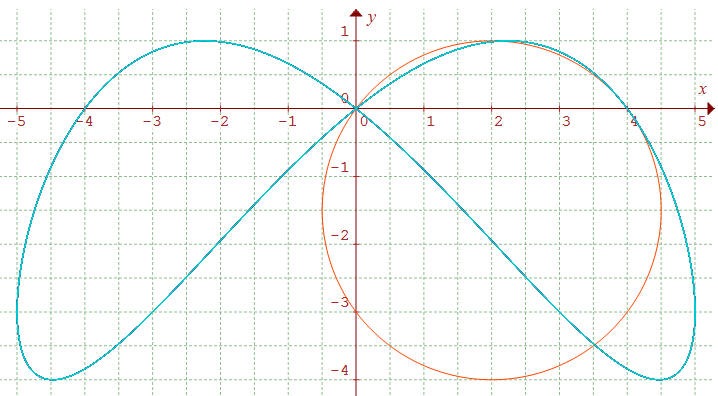
La besace vue par
Graphmatica
(a = 4, b = 3, r = 5/2)
La
courbe est
unicursale,
c'est à dire représentable paramétriquement
sous la forme x = f(t), y = g(t). En
considérant l'équation paramétrique du cercle, x - a/2 = r
× cos t et y
- b/2 = r × sint, on a
: X = (ax + by)1/2
et Y = y, soit :
X = (2r2 + ar.cos t + br.sint)1/2
, Y = b/2 + r.sint ,
t∈[0,2π]
➔
En
posant u = tan(t/2), on pourra exprimer X2 et Y
sous forme de fonctions rationnelle de u.
»
fonction tan
La besace est générée ci-dessous au moyen du logiciel de géométrie dynamique Cabri Géomètre, dans sa
version CabriJava pour Internet :
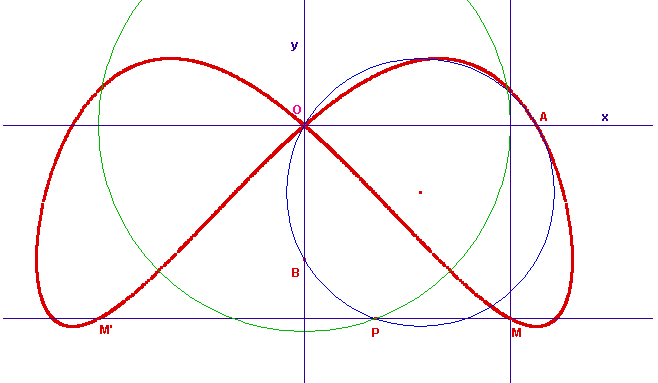

Si votre navigateur accepte les applets
Java (»
extension CheerpJ ) :
) :
Pour générer la courbe, déplacer P; pour effacer le lieu
double-cliquer dans la figure
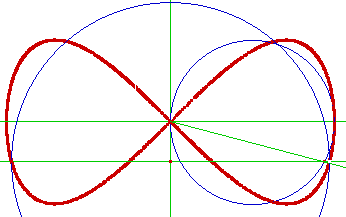
On remarquera que
si b = 0, on obtient un joli nœud papillon qui n'est autre qu'une lemniscate de Gerono
:
© Serge Mehl -
www.chronomath.com






