ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

Aire d'un secteur circulaire, aires latérales du cône, du cylindre, de la pyramide        » Hotte tronc-pyramidale (exercice, aire d'un tronc de pyramide)        » Volume du tronc de cône

1. Aire d'un secteur angulaire :   

Un secteur circulaire est une portion de disque délimitée par deux rayons et l'un des deux arcs de cercles que ces rayons déterminent. L'angle â est l'angle d'ouverture de notre secteur.

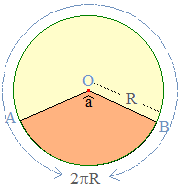
L'aire d'un secteur circulaire est proportionnelle à son angle d'ouverture â. Ci-dessus, par exemple, on s'intéresse au secteur coloré en orange défini par l'arc AB et d'angle saillant â (la mesure de â est inférieure à 180°). On aurait pu s'intéresser au secteur coloré en jaune défini par l'arc AB et d'angle rentrant 360° - â.

La mesure de â étant exprimée en degrés l'aire A du secteur est donnée par la formule :

 A = πR² × â°/360

Lorsque l'angle d'ouverture du secteur est exprimé en radians, notons â_rd sa mesure. La formule d'aire devient  πR² × â_rd/2π, c'est à dire :

A = â_rd × R²/2

En égalisant les deux formules, on peut établir une relation entre les mesures â° et â_rd:

π × â° = 180 × â_rd

On notera que la longueur L d'un arc de cercle AB est, là encore, proportionnelle à l'angle d'ouverture â, ce qui fournit :

2. Aire latérale d'un cône de révolution :    

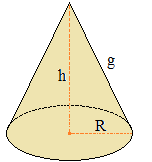Lorsque l'on développe un cône de révolution, de rayon R et de génératrice g (on parle aussi d'apothème), on obtient un secteur circulaire de rayon g.

L'aire latérale d'un tel cône est alors l'aire de ce secteur, laquelle est proportionnelle à l'angle d'ouverture â, donc à la mesure de l'arc AB qui est la circonférence de la base du cône, c'est à dire 2πR.

La circonférence du disque de rayon g étant 2πg, et son aire πg², l'aire latérale A du cône est donnée par la très simple et jolie formule dans laquelle l'angle d'ouverture n'apparaît pas  :

A = πRg

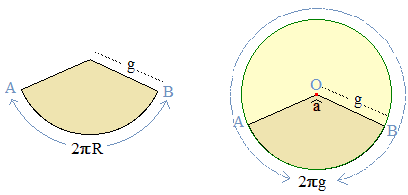
 ➔    Si g n'est pas connu au profit de la hauteur h du cône, on peut calculer g au moyen du théorème de Pythagore.

3. Aire latérale d'un cylindre droit :     

Le patron d'un cylindre droit de rayon R de hauteur h est un rectangle de côtés h et 2πR (périmètre de sa base). L'aire latérale est ainsi 2πRh.

 ➔   L'aire totale (s'il est fermé) est 2 × πR² + 2πRh = 2πR(R + h) et son volume est πR²h.

4. Aire latérale d'une pyramide :   

L'aire latérale d'une pyramide dont la base est un polygone quelconque de n côtés s'obtient en faisant la somme des aires des n triangles constituant ses faces latérales.

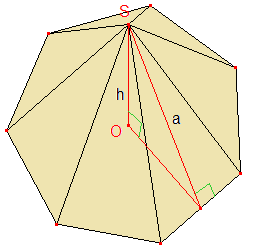
 ➔  Dans le cas particulier où la pyramide est régulière, sa base est un polygone régulier de centre O et son sommet S est situé à la verticale de ce centre (sur la perpendiculaire en O au plan contenant P).

Dans ce cas, chaque face est triangulaire isocèle d'aire commune c × a/2 où a désigne l'apothème de la pyramide (hauteur de chaque face issue de S ) et c la mesure des côtés de la base polygonale régulière. Par conséquent, l'aire latérale est :

A = a × (nc/2) : produit du demi-périmètre de la base par l'apothème.