
ChronoMath, une chronologie des MATHÉMATIQUES
à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges

|
» La théorie et la version JavaScript vous seront exposées en cliquant sur la clé... |
a1,1x1 + a1,2x2 + … + a1,nxn = b1
a2,1x1 + a2,2x2 + … + a2,nxn = b2
…
...
an,1x1 + an,2x2 + … + an,nxn = bn
lorsque celui-ci possède une unique solution : système de Cramer.
Les coefficients ai,j et les bi du système sont fournis par l'utilisateur. Le programme fonctionne au moyen d'une macro écrite en VisualBasic pour Excel, il est en tout point semblable à la version JavaScript :
|
Public Static Sub pivot() If cells(n, n) = 0 Then Call sing: Exit
Sub 'si le dernier
pivot est nul, le système est singulier For i = n - 1 To 1 Step
-1
'calcul des solutions de xn-1 à x1 en
"remontant" cells(li, co) = copi(li, co): Next co: Next li For i = 1 To n 'on affiche le n-uplet des solutions MsgBox ("x(" & i & ") = " & x(i)) Next End Sub Function permu(k)
'permutation de la
ligne k et de la ligne k+1 Public Sub sing()
'le système
est singulier |
| Fenêtre Excel d'exécution : |
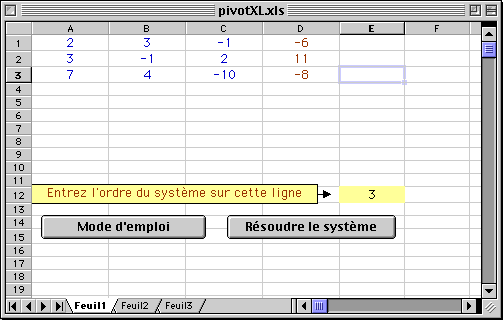
| Exemples d'exécution : |
2x1 + 3x2 - x3 = -6
3x1 - x2 + 2x3 = 11
7x1 + 4x2 - 10x3 = -8
l'ordinateur est désolé.... En effet : L2 = L3 - 2L1.